题目内容
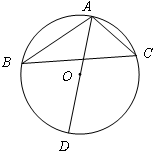
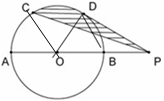
如图:已知AB是⊙O的直径,P为AB的延长线上一点.且BP= AB,C、D是半圆AB的两个三等分点,连接PD.
AB,C、D是半圆AB的两个三等分点,连接PD.

(1)PD与⊙O有怎样的位置关系?并证明你的结论;
(2)连接PC,若AB=10cm,求由PC,弧CD、PD所围成的图形的面积(结果保留π).
 AB,C、D是半圆AB的两个三等分点,连接PD.
AB,C、D是半圆AB的两个三等分点,连接PD.
(1)PD与⊙O有怎样的位置关系?并证明你的结论;
(2)连接PC,若AB=10cm,求由PC,弧CD、PD所围成的图形的面积(结果保留π).
(1)相切;(2)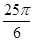
试题分析:(1)连结OD、BD,由BP=
 AB ,OB=
AB ,OB= AB可证得BP=OB,再根据C、D是半圆AB的两个三等分点可得∠DOB=∠COD="60°" ,即可BD=OB=BP,从而证得结论;
AB可证得BP=OB,再根据C、D是半圆AB的两个三等分点可得∠DOB=∠COD="60°" ,即可BD=OB=BP,从而证得结论;(2)连接CO,由∠COD="60°" ,CO=OD可得CO=OD=CD,即可证得CD∥AB,根据平行线的性质及三角形的面积公式可得
 ,从而可以求得结果.
,从而可以求得结果.(1)PD与⊙O相切,理由如下
连结OD、BD
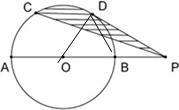
∵BP=
 AB ,OB=
AB ,OB= AB
AB∴BP=OB
∵C、D是半圆AB的两个三等分点
∴∠DOB=∠COD="60°"
∵OD=OB
∴BD=OB=BP
∴∠ODP=90°
∴PD与⊙O相切;
(2)连接CO
∵∠COD="60°" ,CO=OD
∴CO=OD=CD
∴∠DOB=∠CDO=60°
∴CD∥AB
∴

∴
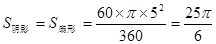 .
.点评:此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目

 时(如图),求证:CD是⊙O的切线;
时(如图),求证:CD是⊙O的切线; 轴上.
轴上.
 中,
中, ,
, .
. 是
是 的中点,⊙
的中点,⊙ 与点
与点 .与
.与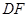 并延长交
并延长交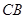 的延长线于点
的延长线于点 .若
.若 ,则
,则 __.
__.


 的半径为5,
的半径为5, 为⊙
为⊙ ⊥
⊥ .若
.若 ,则
,则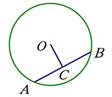
 ,
, ,则
,则 的长度是 .
的长度是 .