题目内容
如图,△ABC的3个顶点都在⊙O上,直径 ,
, ,则
,则 的长度是 .
的长度是 .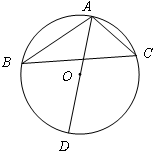
 ,
, ,则
,则 的长度是 .
的长度是 .
1
试题分析:连接AD,根据圆周角定理可得∠ACD=90°,∠B=∠D=30°,再根据含30°的直角三角形的性质求解即可.
连接AD
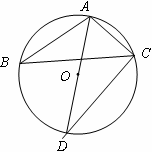
∵直径
 ,
,
∴∠ACD=90°,∠B=∠D=30°
∴Ac=1.
点评:解题的关键是熟练掌握含30°的直角三角形的性质:30°角所对的直角边等于斜边的一半.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
题目内容
 ,
, ,则
,则 的长度是 .
的长度是 .

 ,
,

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案