题目内容
如图所示,已知A点的坐标为(0,3),⊙A的半径为1,点B在 轴上.
轴上.

①若点B的坐标为(4,0),⊙B的半径为3,试判断⊙A与⊙B的位置关系;
②能否在 轴的正半轴上确定一点B,使⊙B与y轴相切,并且与⊙A相切?请说明理由.
轴的正半轴上确定一点B,使⊙B与y轴相切,并且与⊙A相切?请说明理由.
 轴上.
轴上.
①若点B的坐标为(4,0),⊙B的半径为3,试判断⊙A与⊙B的位置关系;
②能否在
 轴的正半轴上确定一点B,使⊙B与y轴相切,并且与⊙A相切?请说明理由.
轴的正半轴上确定一点B,使⊙B与y轴相切,并且与⊙A相切?请说明理由.(1)外离 (2)B(4,0)
试题分析:(1)根据题意得已知A点的坐标为(0,3),在y轴的正半轴上;若点B的坐标为(4,0),它在
 轴的正半轴上,那么⊙A、⊙B的圆心距=
轴的正半轴上,那么⊙A、⊙B的圆心距=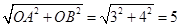 ,由⊙A的半径为1,⊙B的半径为3,半径之和为1+3=4,因为5>1+3=4,所以⊙A与⊙B的位置关系是外离
,由⊙A的半径为1,⊙B的半径为3,半径之和为1+3=4,因为5>1+3=4,所以⊙A与⊙B的位置关系是外离(2)假设在
 轴的正半轴上确定一点B,设B(x,0),根据题意得,使⊙B与y轴相切,⊙B的半径为x,因为使⊙B与⊙A相切,所以⊙A、⊙B的圆心距=⊙A、⊙B的圆心距的半径之和,因为⊙A、⊙B的圆心距=
轴的正半轴上确定一点B,设B(x,0),根据题意得,使⊙B与y轴相切,⊙B的半径为x,因为使⊙B与⊙A相切,所以⊙A、⊙B的圆心距=⊙A、⊙B的圆心距的半径之和,因为⊙A、⊙B的圆心距=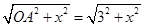 ,⊙A、⊙B的圆心距的半径之和=1+x,所以
,⊙A、⊙B的圆心距的半径之和=1+x,所以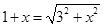 ,解得x=4,所以B点的坐标为(4,0)
,解得x=4,所以B点的坐标为(4,0)点评:本题考查两圆相离、相切,考生解答本题的关键是掌握两圆的位置关系,熟悉两圆相离、相切的概念和性质,掌握勾股定理的内容

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 cm,轴截面上有两点P、Q,PA=40cm,BQ=30cm,则圆柱的侧面上P、Q两点的最短距离是 .
cm,轴截面上有两点P、Q,PA=40cm,BQ=30cm,则圆柱的侧面上P、Q两点的最短距离是 .

 EF,垂足为G,∠OEG=30°,则∠DCF= .
EF,垂足为G,∠OEG=30°,则∠DCF= .
 AB,C、D是半圆AB的两个三等分点,连接PD.
AB,C、D是半圆AB的两个三等分点,连接PD.
 中,
中,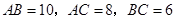 ,经过点
,经过点 且与边
且与边 相切的动圆与
相切的动圆与 分别相交于点
分别相交于点 ,则线段
,则线段 长度的最小值是( )
长度的最小值是( )

