题目内容
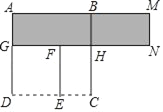
【题目】如图,四边形ABCD与四边形DEFG都是正方形,设AB=a,DE=b(a>b).
(1)写出AG的长度(用含字母a,b的代数式表示);
(2)观察图形,当用不同的方法表示图形中阴影部分的面积时,你能获得一个因式分解公式,请将这个公式写出来;
(3)如果正方形ABCD的边长比正方形DEFG的边长多16cm,它们的面积相差960cm2,试利用(2)中的公式,求a,b的值.
【答案】(1)AG=a﹣b;(2)能;a2﹣b2=(a+b)(a﹣b);(3)a的长为38cm,b的长为22cm;
【解析】
(1)结合图形,由线段间的和差关系进行计算即可;
(2)图中阴影部分的面积=大正方形的面积-小正方形的面积;或者把阴影部分分割为两个矩形的面积进行计算;
(3)利用(2)中的平方差公式进行计算.
(1)AG=a﹣b;
(2)能. a2﹣b2或a(a﹣b)+b(a﹣b);
a2﹣b2=a(a﹣b)+b(a﹣b)=(a+b)(a﹣b),
即a2﹣b2=(a+b)(a﹣b);
(3)由题意,得a﹣b=16①,
a2﹣b2=(a+b)(a﹣b)=960,
∴a+b=60②,
由 ①、②方程组解得a=38,b=22.
故a的长为38cm,b的长为22cm

练习册系列答案
相关题目