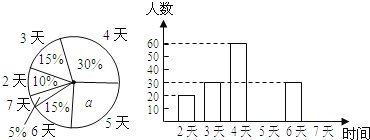
题目内容
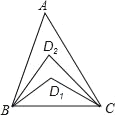
【题目】如图，在△ABC中，∠A＝20°，∠ABC与∠ACB的角平分线交于D1，∠ABD1与∠ACD1的角平分线交于点D2，依此类推，∠ABD4与∠ACD4的角平分线交于点D5，则∠BD5C的度数是_____．
【答案】25°
【解析】
根据题意可得∠ABC+∠ACB＝160°，BD1，CD1，CD2，BD2…BDn，CDn是角平分线，可得∠ABDn+∠ACDn＝160×（
）n，可求∠BCDn+∠CBDn的值，再根据三角形内角和定理可求结果．
∵∠A＝20°，∠A+∠ABC+∠ACB＝180°，
∴∠ABC+∠ACB＝160°，
∵BD1平分∠ABC，CD1平分∠ACB，
∴∠ABD1＝ABC，∠ACD1＝∠ACD，
∵BD2平分∠ABD1，CD2平分∠ACD1
∴∠ABD2＝∠ABD1＝
∠ABC，∠ACD2＝∠ACD1＝∠ACB，
同理可得∠ABD5＝
∠ABC，∠ACD5＝∠ACB，
∴∠ABD5+∠ACD5＝160×＝5°，
∴∠BCD5+∠CBD5＝155°，
∴∠BD5C＝180﹣∠BCD5﹣∠CBD5＝25°
故答案为25°
练习册系列答案
相关题目
