题目内容
【题目】如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交![]() 于点D,过点D作⊙O的切线,交BA的延长线于点E.
于点D,过点D作⊙O的切线,交BA的延长线于点E.
(1)求证:AC∥DE;
(2)连接CD,若OA=AE=1,求四边形ACDE面积.

【答案】(1)证明见解析;(2)![]()
【解析】(1)欲证明AC∥DE,只要证明AC⊥OD,ED⊥OD即可.
(2)作DM⊥OA于M,连接CD,CO,AD,首先证明四边形ACDE是平行四边形,根据S平行四边形ACDE=AEDM,只要求出DM即可.
(1)证明:∵ED与⊙O相切于D,∴OD⊥DE,
∵F为弦AC中点,∴OD⊥AC,∴AC∥DE.
(2)解:作DM⊥OA于M,连接CD,CO,AD.
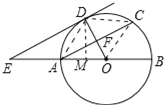
∵AC∥DE,AE=AO,∴OF=DF,
∵AF⊥DO,∴AD=AO,∴AD=AO=OD,
∴△ADO是等边三角形,同理△CDO也是等边三角形,
∴∠CDO=∠DOA=60°,AE=CD=AD=AO=DD=1,
∴AO∥CD,又AE=CD,
∴四边形ACDE是平行四边形,易知DM=![]() ,
,
∴平行四边形ACDE面积=![]() .
.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目