题目内容
【题目】AD是△ABC的边BC上的中线,AB=12,AC=8,则边BC的取值范围是_______________________;中线AD的取值范围是__________________.
【答案】4<BC<20 , 2<AD<10
【解析】BC边的取值范围可在△ABC中利用三角形的三边关系进行求解,而对于中线AD的取值范围可延长AD至点E,使AD=DE,得出△ACD≌△EBD,进而在△ABE中利用三角形三边关系求解.
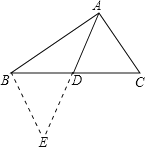
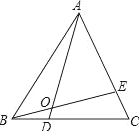
解:如图所示,
在△ABC中,则AB-AC<BC<AB+AC,
即12-8<BC<12+8,4<BC<20,
延长AD至点E,使AD=DE,连接BE,
∵AD是△ABC的边BC上的中线,∴BD=CD,
又∠ADC=∠BDE,AD=DE
∴△ACD≌△EBD,∴BE=AC,
在△ABE中,AB-BE<AE<AB+BE,即AB-AC<AE<AB+AC,
12-8<AE<12+8,即4<AE<20,
∴2<AD<10.
故此题的答案为4<BC<20,2<AD<10.
本题主要考查了全等三角形的判定及性质以及三角形的三边关系问题,能够理解掌握并熟练运用.

练习册系列答案
相关题目