题目内容
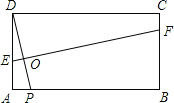
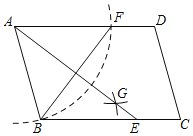
【题目】如图，在ABCD中，以点A为圆心AB长为半径作弧交AD于点F，分别以点B、F为圆心，同样长度m为半径作弧，交于点G，连结AG并延长交BC于点E，若BF＝6，AB＝4，则AE的长为_____．
【答案】
【解析】
连接FE，设AE交BF于点O．首先证明四边形ABEF是菱形，利用勾股定理求出AO即可．
如图，连接FE，设AE交BF于点O．
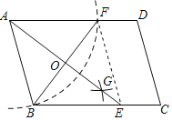
由作图可知：AB＝AF，AE平分∠BAD，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠FAE＝∠AEB＝∠BAE，
∴AB＝BE，
∴AF＝BE，
又∵AF∥BE，
∴四边形ABEF是平行四边形，
∵AB＝AF，
∴四边形ABEF是菱形，
∴AE⊥BF，
∴AO＝OE＝
AE，BO＝OF＝3，
在Rt△AOB中，AO＝
，
∴AE＝2OA＝．
故答案是：．
练习册系列答案
相关题目
