Question

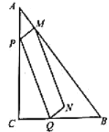
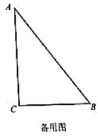
【题目】如图，已知在中，，，，点、分别在边、射线上，且，过点作，垂足为点，联结，以、为邻边作平行四边形，设，平行四边形的面积为．

（1）当平行四边形为矩形时，求的正切值；

（2）当点在内，求关于的函数解析式，并写出它的定义域；

（3）当过点且平行于的直线经过平行四边形一边的中点时，直接写出的值．

Answer 1

【答案】（1）；（2）；（3），．

【解析】

（1）当四边形PQMN是矩形时，PQ∥AB．根据tan∠PQM＝求解即可．

（2）如图1中，延长QN交AB于K．求出MK，PM，根据y＝PMMK求解即可．

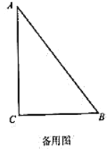
（3）分两种情形：①如图31中，当平分MN时，D为MN的中点，作NE∥BC交PQ于E，作NH⊥CB交CB的延长线于H，EG⊥BC于G．根据EG＝PC构建方程求解．②如图32中，当平分NQ时，D是NQ的中点，作DH⊥CB交CB的延长线于H．根据PC＝GH构建方程求解即可．

（1）在Rt△ACB中，∵∠C＝90，AC＝8，BC＝6，

∴AB＝＝＝10，

当四边形PQMN是矩形时，PQ∥AB．

∴tan∠PQM＝＝．

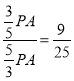（2）如图1中，延长QN交AB于K．

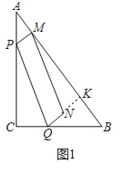
∵∠C＝90，AC＝8，BC＝6，AB=10

∴sinA=cosB==,cosA=sinB=，

由，得BQ＝6x，QN＝PM＝APsinA=x，AM＝APcosA=x，KQ＝BQsinB=BQ＝，BK＝BQcosB=BQ＝，

∴MK＝ABAMBK＝，

∵QN＜QK，

∴x＜，

∴x＜，

∴y＝PMMK＝x×=（0≤x＜）．

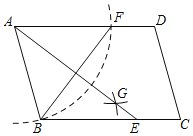
（3）①如图31中，当平分MN时，D为MN的中点，作NE∥BC交PQ于E，作NH⊥CB交CB的延长线于H，EG⊥BC于G．

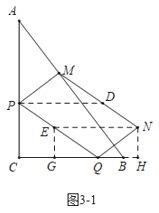
∵PD∥BC，EN∥BC，

∴PD∥NE，

∵PE∥DN，

∴四边形PDNE是平行四边形，

∴PE＝DN，

∵DN＝DM，PQ＝MN，

∴PE＝EQ，

∵EG∥PC，

∴CG＝GQ，

∴EG＝PC，

∵四边形EGHN是矩形，

∵

∴QN⊥AB

则∠ABC+∠NQH=∠NQH +∠QNH=90°

∴∠ABC=∠QNH

∴NH＝EG＝NQcos∠QNH= NQcos∠ABC =NQ＝PM＝×x =x，PC＝8x，

∴x＝（8x），

解得x＝．

②如图32中，当平分NQ时，D是NQ的中点，作DH⊥CB交CB的延长线于H．

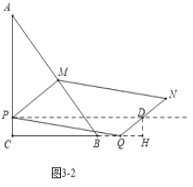
∵DH＝PC，

∴8x＝x，

解得x＝，

综上所述，满足条件x的值为或．