题目内容
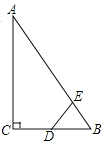
【题目】如图，Rt△ABC中，
，
，
，D为BC的中点，若动点E以1cm/s的速度从A点出发，沿AB向B点运动，设E点的运动时间为t秒，连接DE，当以B、D、E为顶点的三角形与△ABC相似时，t的值为（ ）
A.2或3.5B.2或3.2C.2或3.4D.3.2或3.4
【答案】A
【解析】
求出AB=2BC=4cm，分两种情况：①当∠EDB=∠ACB=90°时，DE∥AC，△EBD∽△ABC，得出AE=BE=
AB=2cm，即可得出t=2s；②当∠DEB=∠ACB=90°时，证出△DBE∽△ABC，得出∠BDE=∠A=30°，因此BE=BD=cm，得出AE=3.5cm，t=3.5s；即可得出结果．
解：∵∠ACB=90°，∠ABC=60°，
∴∠A=30°，
∴AB=2BC=4cm，
分两种情况：
①当∠EDB=∠ACB=90°时，
DE∥AC，所以△EBD∽△ABC，
E为AB的中点，AE=BE=AB=2cm，
∴t=2s；
②当∠DEB=∠ACB=90°时，
∵∠B=∠B，
∴△DBE∽△ABC，
∴∠BDE=∠A=30°，
∵D为BC的中点，
∴BD=BC=1cm，
∴BE=BD=0.5cm，
∴AE=3.5cm，
∴t=3.5s；
综上所述，当以B、D、E为顶点的三角形与△ABC相似时，t的值为2或3.5，
故选：A.
练习册系列答案
相关题目
