��Ŀ����
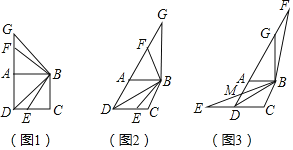
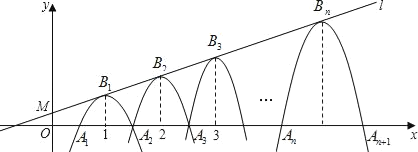
����Ŀ�����壺�������ߵĶ�����x����������㹹�ɵ���������ֱ�������Σ������������߱���Ϊ����ֱ�������ߡ�����ͼ��ֱ��l��y��![]() x+b������M(0��
x+b������M(0��![]() )��һ�������ߵĶ���B1(1��y1)��B2(2��y2)��B3(3��y3)����Bn(n��yn)��(nΪ������)��������ֱ��l�ϵĵ㣬��һ����������x��������Ľ���A1(x1��0)��A2(x2��0)���ڶ�����������x�ύ��A2(x2��0)��A3(x3��0)���Դ����ƣ���x1��d(0��d��1)����dΪ_____ʱ�������������д���ֱ�������ߣ�
)��һ�������ߵĶ���B1(1��y1)��B2(2��y2)��B3(3��y3)����Bn(n��yn)��(nΪ������)��������ֱ��l�ϵĵ㣬��һ����������x��������Ľ���A1(x1��0)��A2(x2��0)���ڶ�����������x�ύ��A2(x2��0)��A3(x3��0)���Դ����ƣ���x1��d(0��d��1)����dΪ_____ʱ�������������д���ֱ�������ߣ�
���𰸡�![]() ��
��![]() ��
��![]()
��������
�������ߵĶԳ��Կ�֪�������ɵ�ֱ�������α����������߶���Ϊֱ�Ƕ���ĵ��������Σ����Դ˵���������б���ϵĸߵ���б�ߵ�һ�룮��0��d��1�����Ե���ֱ��������б�ߵij�С��2�����Ե���ֱ��������б�ߵĸ�һ��С��1���������ߵĶ���������ض�С��1��
ֱ��l��y��![]() x+b������M(0��
x+b������M(0��![]() )����b��
)����b��![]() ��
��
��ֱ��l��y��![]() ��
��
�������ߵĶԳ���֪�������ߵĶ�����x����������㹹�ɵ�ֱ�������α�Ϊ����ֱ�������Σ�
��õ��������εĸߵ���б�ߵ�һ�룮
��0��d��1��
��õ���ֱ�������ε�б�߳�С��2��б���ϵĸ�С��1(�������ߵĶ���������С��1)��
��x��1ʱ��![]() ��
��
��x��2ʱ��![]() ��
��
��x��3ʱ��![]() ��
��
��x��4ʱ��![]() ��
��
��ֱ�������ߵĶ���ֻ��B1��B2��B3��
����B1Ϊ���㣬��![]() ����
����![]() ��
��
����B2Ϊ���㣬��![]() ����
����![]() ��
��
����B3Ϊ���㣬��![]() ����d��
����d��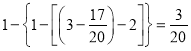 ��
��
����������d��ֵΪ![]() ��
��![]() ��
��![]() ʱ�������������д���ֱ�������ߣ�
ʱ�������������д���ֱ�������ߣ�
�ʴ�Ϊ��![]() ��
��![]() ��
��![]() ��
��