Question

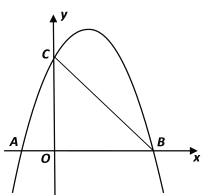
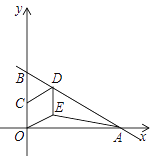
【题目】如图，直线与x轴、y轴分别交于A，B两点，C是OB的中点，D是AB上一点，四边形OEDC是菱形，则△OAE的面积为________．

Answer 1

【答案】

【解析】分析: 根据直线于坐标轴交点的坐标特点得出,A,B两点的坐标，得出OB，OA的长，根据C是OB的中点，从而得出OC的长，根据菱形的性质得出DE=OC=2;DE∥OC；设出D点的坐标，进而得出E点的坐标，从而得出EF,OF的长，在Rt△OEF中利用勾股定理建立关于x的方程，求解得出x的值，然后根据三角形的面积公式得出答案.

详解: 把x=0代入 y = x + 4 得出y=4,

∴B(0,4);

∴OB=4;

∵C是OB的中点，

∴OC=2,

∵四边形OEDC是菱形,

∴DE=OC=2;DE∥OC,

把y=0代入 y = x + 4 得出x=,

∴A(,0);

∴OA=,

设D(x,) ,

∴E(x,- x+2),

延长DE交OA于点F，

∴EF=-x+2,OF=x,

在Rt△OEF中利用勾股定理得：,

解得 ：x1=0(舍），x2=；

∴EF=1,

∴S△AOE=·OA·EF=2.

故答案为：.