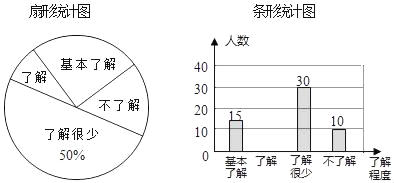
题目内容
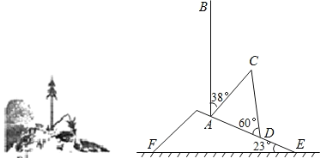
【题目】如图所示,一透明的敞口正方体容器ABCD﹣A'B'C'D'装有一些液体,棱AB始终在水平桌面上,液面刚好过棱CD,并与棱BB'交于点Q.此时液体的形状为直三棱柱,其三视图及尺寸见下图所示请解决下列问题:
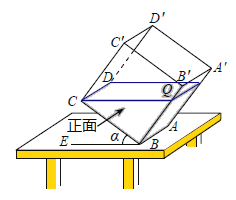
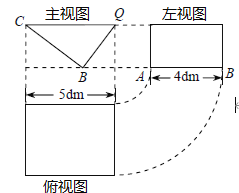
(1)CQ与BE的位置关系是 ,BQ的长是 dm:
(2)求液体的体积;(提示:直棱柱体积=底面积×高)
(3)若容器底部的倾斜角∠CBE=α,求α的度数.(参考数据:sin49°=cos41°=![]() ,tan37°=
,tan37°=![]() )
)
【答案】(1)平行,3;(2)V液=24(dm3);(3)α=37°.
【解析】
(1)如图可直接得到CQ与BE的位置关系,再由勾股定理求BQ的长;
(2)根据三视图得到直三棱柱的边长,再由直棱柱体积=底面积×高,即可求得;
(3)根据两直线平行内错角相等和三角函数值,即可求得![]() .
.
(1)CQ∥BE,BQ=![]() =3dm.
=3dm.
(2)V液=![]() ×3×4×4=24(dm3).
×3×4×4=24(dm3).
(3)∵CQ∥BE,
∴∠CBE=∠BCQ,
∵在Rt△BCQ中,tan∠BCQ=![]() =
=![]() ,
,
∴∠BCQ=37°,
∴α=∠BCQ=37°.

 阅读快车系列答案
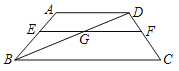
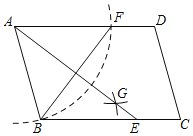
阅读快车系列答案【题目】如图,∠MAN=30°,在射线AN上取一点B,使AB=4 cm,过点B作BC⊥AM于点C,点D为边AB上的动点(点D不与点A,点B重合),连接CD,过点D作ED⊥CD交直线AC于点E.在点D由点A到点B运动过程中,设AD=x cm,AE=y cm.
(1)取指定点作图,根据下面表格预填结果,先通过作图确定AD=2 cm时,点E的位置,测量AE的长度.
①根据题意,在答题卡上补全图形;
②把表格补充完整:通过取点、画图、测量,得到了x与y的几组对应值,如表:
x/cm | … |
| 1 |
| 2 |
| 3 |
| … |
y cm | … | 0.4 | 0.8 | 1.0 | m | 1.0 | 0 | 4.0 | … |
则m=______(结果保留一位小数).
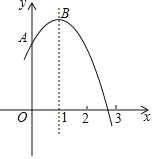
(2)在下面的平面直角坐标系xOy中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当AE=![]() AD时,AD的长度约为______cm.
AD时,AD的长度约为______cm.