Question

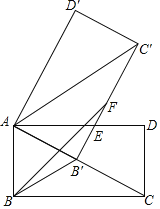
【题目】如图，在矩形ABCD中，AB＝3，AD＝1，点P在线段AB上运动，设AP＝，现将纸片折叠，使点D与点P重合，得折痕EF（点E、F为折痕与矩形边的交点），再将纸片还原．

（1）当＝0时，折痕EF的长为　 　；当点E与点A重合时，折痕EF的长为　　；

（2）请写出使四边形EPFD为菱形的的取值范围，并求出当＝2时菱形的边长；

（3）令EF2＝，当点E在AD、点F在BC上时，写出与的函数关系式．当取最大值时，判断△EAP与△PBF是否相似？若相似，求出的值；若不相似，请说明理由．温馨提示：用草稿纸折折看，或许对你有所帮助哦！

Answer 1

【答案】（1）3；；（2）1≤≤3，时菱形边长为；（3）＝92+9；当取最大值时△EAP∽△PBF，＝3﹣2．

【解析】

（1）当＝0时，点A与点P重合，则折痕EF的长等于矩形ABCD中的AB的长；当点E与点A重合时，折痕是以AD为边的正方形的角平分线，可求EF＝；

（2）由题意可知，要想使四边形EPFD为菱形，则EF与DP互相垂直平分线段，所以点E必须要在线段AB上，点F必须在线段DC上，由此确定的取值范围．再利用勾股定理确定菱形的边长；

（3）构造直角三角形，利用相似三角形的对应线段成比例确定的值，再利用二次函数的增减性确定的最大值．

（1）当＝0时，折痕EF＝AB＝3；

当点E与点A重合时，折痕EF＝．

（2）1≤≤3．

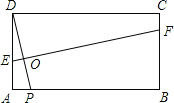
当＝2时，如图1，连接DE、PF．

∵EF为折痕，

∴DE＝PE，

令PE为m，则AE＝2-m，DE＝m，

在Rt△ADE中，AD2+AE2＝DE2

∴1+(2-m)2＝m2，解得m＝；

此时菱形边长为．

（3）如图2，过E作EH⊥BC；

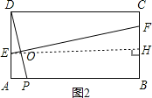
∵△EFH∽△DPA，

∴，即

∴FH＝3x；

∴＝EF2＝FH2+EH2＝92+9；

当F与点C重合时，如图3，连接PF；

∵PF＝DF＝3，

∴PB＝，

∴0≤≤3-；

∵函数＝92+9的值在轴的右侧随的增大而增大，

∴当＝3-时，有最大值，

此时∠EPF＝90°，△EAP∽△PBF．

综上所述，当取最大值时△EAP∽△PBF，＝3-．