题目内容
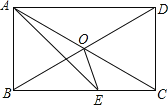
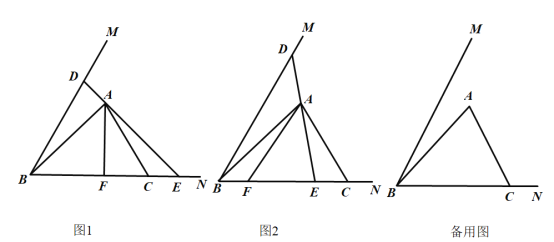
【题目】如图,点P在平行四边形ABCD的边BC上,将△ABP沿直线AP翻折,点B恰好落在边AD的垂直平分线上,如果AB=5,AD=8,tanB=![]() ,那么BP的长为_____.
,那么BP的长为_____.
【答案】![]() 或7
或7
【解析】
①如图1,过A作AH⊥BC于H,连接DB′,设AH=4x,BH=3x,根据勾股定理得到AB=![]() =5x=5,根据旋转的性质得到AB′=AB=5,AM=DM=
=5x=5,根据旋转的性质得到AB′=AB=5,AM=DM=![]() AD=4,∠AMN=∠HNM=90°,根据勾股定理得到MB′=
AD=4,∠AMN=∠HNM=90°,根据勾股定理得到MB′=![]() =3,求得HN=MN=4,根据相似三角形的性质即可得到结论;
=3,求得HN=MN=4,根据相似三角形的性质即可得到结论;
②如图2,由①知,MN=4,MB′=3,BN=7,求得NB=NB′,推出点P与N重合,得到BP=BN=7.
①如图1,过A作AH⊥BC于H,连接DB′,

设BB′与AP交于E,
AD的垂直平分线交AD于M,BC于N,
∵tanB=![]() ,
,
∴设AH=4x,BH=3x,
∴AB=![]() =5x=5,
=5x=5,
∴x=1,
∴AH=4,BH=3,
∵将△ABP沿直线AP翻折,点B恰好落在边AD的垂直平分线MN上,
∴AB′=AB=5,AM=DM=![]() AD=4,∠AMN=∠HNM=90°,
AD=4,∠AMN=∠HNM=90°,
∴四边形AHNM是正方形,MB′=![]() =3,
=3,
∴HN=MN=4,
∴BN=7,B′N=1,
∴BB′=![]() ,
,
∴BE=![]() BB′=
BB′=![]() ,
,
∵∠BEP=∠BNB′=90°,∠PBE=∠B′BN,
∴△BPE∽△BB′N,
∴![]() ,
,
∴![]() ,
,
∴BP=![]() ;
;
②如图2,由①知,MN=4,MB′=3,BN=7,
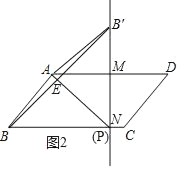
∴NB=NB′,
∴点N在BB′的垂直平分线上,
∵将△ABP沿直线AP翻折,点B恰好落在边AD的垂直平分线上,
∴点P也在BB′的垂直平分线上,
∴点P与N重合,
∴BP=BN=7,
综上所述,BP的长为![]() 或7.
或7.
故答案为:![]() 或7.
或7.

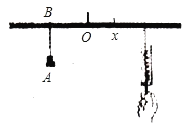
【题目】如图,小华设计了一个探索杠杆平衡的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O的右侧用一个弹簧秤向下拉木杆,改变弹簧秤与点O的距离x(单位:厘米),观察弹簧秤的示数y(单位:牛)的变化情况,实验数据记录如下:
x(单位:厘米) | … | 10 | 15 | 20 | 25 | 30 | … |
y(单位:牛) | … | 30 | 20 | 15 | 12 | 10 | … |
(1)请写出一个符合表格中数据x关于y的函数关系;
(2)当弹簧秤的示数为30牛时,弹簧秤与点O的距离是多少厘米?随着弹簧秤与O点的距离不断减小,弹簧秤的示数将发生怎样的变化?