Question

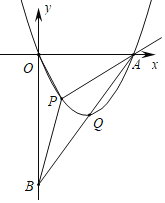
【题目】如图，抛物线与轴交于点和点，与轴交于点，作直线，点的坐标为，点的坐标为．

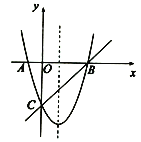
（1）求抛物线的解析式并写出其对称轴；

（2）为抛物线对称轴上一点，当是以为直角边的直角三角形，求点坐标；

（3）若为轴上且位于点下方的一点，为直线上的一点，在第四象限的抛物线上是否存在一点．使以为顶点的四边形是菱形且为菱形对角线？若存在，请求出点的横坐标；若不存在，请说明理由．

Answer 1

【答案】（1），对称轴；（2）点或；（3）点．

【解析】

（1）将点B、C的坐标代入二次函数表达式，即可求解；

（2）分∠BCD＝90、∠DBC＝90两种情况，分别求解即可；

（3）根据CE为菱形的对角线时，PQ⊥CE，即PQ∥x轴，再根据CQ=CP得到方程组，联立即可求解．

解：（1）将点的坐标代入二次函数表达式得：，

解得：，

故抛物线的表达式为：，

令，则或6，则点，

则函数的对称轴；

（2）①当时，

设BC的解析式为y=kx+b，

把B、 代入得

解得

∴直线的表达式为：，

∵BC⊥CD，

∴可设直线CD为y=-x+d

把 代入y=-x+d得-6=d，

∴直线的表达式为：，

当时，，故点；

②当时，

直线的表达式为：，

∵BD⊥CD，

∴可设直线BD为y=-x+e

把B代入y=-x+e得0=-6+e，

∴e=6

∴直线BD的表达式为：，

当时，，故点，

故点或；

（3）由题意知为菱形的对角线，

则，即轴，

设点，则点，

把Q代入抛物线得…①，

∵直线的表达式为：，

∴∠CPE=45°，

∴△PCE是等腰直角三角形，

∵PE=-m，

∴，

∵EQ=s，CE= PE=-m

∴，

由题意得：，即：…②

联立①②并解得：或-2（舍去6）

故点；

∴点．