题目内容
【题目】已知锐角![]() 的余弦值为
的余弦值为![]() ,点
,点![]() 在射线
在射线![]() 上,
上,![]() ,点
,点![]() 在
在![]() 的内部,且
的内部,且![]() ,
,![]() .过点
.过点![]() 的直线
的直线![]() 分别交射线
分别交射线![]() 、射线
、射线![]() 于点
于点![]() 、
、![]() .点
.点![]() 在线段
在线段![]() 上(点
上(点![]() 不与点
不与点![]() 重合),且
重合),且![]() .
.
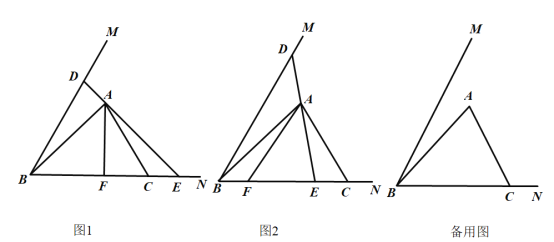
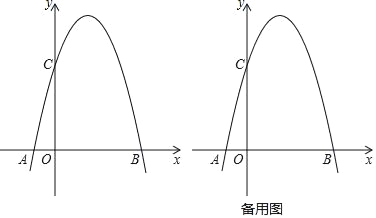
(1)如图1,当![]() 时,求
时,求![]() 的长;
的长;
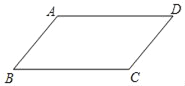
(2)如图2,当点![]() 在线段
在线段![]() 上时,设
上时,设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数解析式并写出函数定义域;
的函数解析式并写出函数定义域;
(3)联结![]() ,当
,当![]() 与
与![]() 相似时,请直接写出
相似时,请直接写出![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]()
![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)由锐角三角函数可求AC=15,根据勾股定理和三角形面积公式可求AB,AF的长,即可求EF的长;
(2)通过证△FAE∽△FCA和△BDE∽△CFA,可得y关于x的函数解析式;
(3)分△ADF∽△CEA,△ADF∽△CAE两种情况讨论,通过等腰三角形的性质和相似三角形性质可求BD的长.
解:(1)![]() 在
在![]() 中
中![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
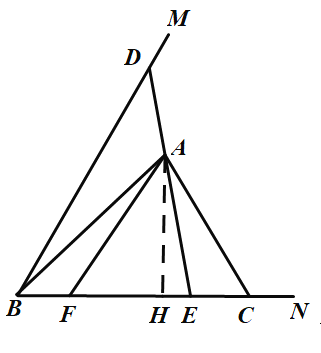
(2)过点![]() 作
作![]() 于点
于点![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]() ,
,
![]()
又![]() ,
,![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
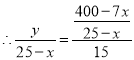
![]()
![]()
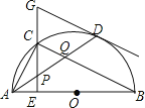
(3)如图,若△ADF∽△CAE,
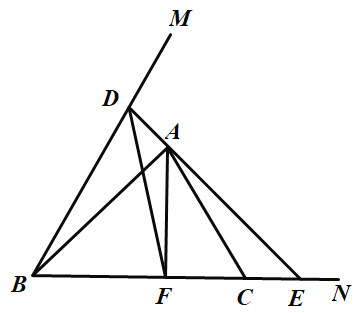
∵△△ADF∽△CEA,
∴∠ADF=∠AEC,
∵∠EAF=∠MBN,∠EAF+∠DAF=180°,
∴∠DAF+∠MBN=180°,
∴点A,点F,点B,点D四点共圆,
∴∠ADF=∠ABF,
∴∠ADF=∠AEC=∠ABF,
∴AB=AE,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,且∠ABF=∠AEC,∠ACB=∠MBN=∠EAF,
∴∠AEC+∠EAF=90°,∠AEC+∠MBN=90°,
∴∠BDE=90°=∠AFC,
∵S△ABC=![]() ×AB×AC=
×AB×AC=![]() ×BC×AF,
×BC×AF,
∴AF![]() ,
,
∴BF=![]() ,
,
∵AB=AE,∠AFC=90°,
∴BE=2BF=32,
∴cos∠MBN=![]() ,
,
∴BE=![]() ,
,
如图,若△ADF∽△CAE,
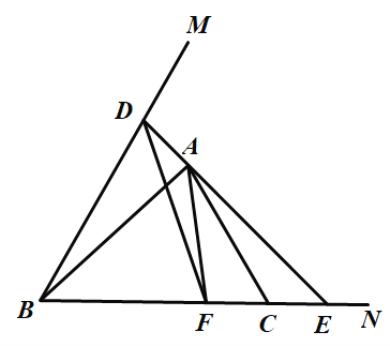
∵△ADF∽△CAE,
∴∠ADF=∠CAE,∠AFD=∠AEC,
∴AC//DF
∴∠DFB=∠ACB,且∠ACB=∠MBN,
∴∠MBN=∠DFB,
∴DF=BD,
∵∠EAF=∠MBN,∠EAF+∠DAF=180°,
∴∠DAF+∠MBN=180°,
∴点A,点F,点B,点D四点共圆,
∴∠ADF=∠ABF,
∴∠CAE=∠ABF,且∠AEC=∠AEC,
∴△ABE∽△CAE
∴![]()
设CE=3k,AE=4k,(k≠0)
∴BE=![]() ,
,
∵BC=BECE=25
∴k=![]()
∴AE=![]() ,CE=
,CE=![]() ,BE=
,BE=![]()
∵∠ACB=∠FAE,∠AFC=∠AFE,
∴△AFC∽△EFA,
∴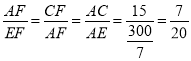 ,
,
设AF=7a,EF=20a,
∴CF=![]() ,
,
∵CE=EFCF=![]() ,
,
∴a=![]() ,
,
∴EF=![]() ,/p>
,/p>
∵AC//DF,
∴![]() ,
,
∴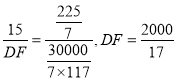 ,
,
故答案为:![]() 或
或![]()

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案