题目内容
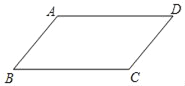
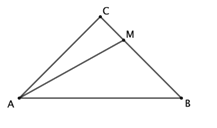
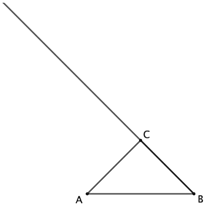
【题目】如图,在等腰直角![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一动点,连接
上一动点,连接![]() ,以点
,以点![]() 为中心,将线段
为中心,将线段![]() 顺时针旋转135°,得到线段
顺时针旋转135°,得到线段![]() ,连接
,连接![]() .
.
(1)依题意,补全图形;
(2)求证:![]() ;
;
(3)点![]() 在线段
在线段![]() 的延长线上,点
的延长线上,点![]() 是点
是点![]() 关于点
关于点![]() 的对称点,写出
的对称点,写出![]() 的一个值,使得对任意的点
的一个值,使得对任意的点![]() 总有
总有![]() ,并证明.
,并证明.
【答案】(1)补图见解析;(2)证明见解析;(3)![]() ,证明见解析
,证明见解析
【解析】
(1)先根据旋转的性质画出![]() ,再连接BN即可;
,再连接BN即可;
(2)先根据等腰三角形的性质得出![]() ,再根据三角形的内角和定理得出
,再根据三角形的内角和定理得出![]() ,然后根据旋转的性质得出
,然后根据旋转的性质得出![]() ,由此即可得证;
,由此即可得证;
(3)如图(见解析),作点![]() 关于
关于![]() 的对称点
的对称点![]() ,连接
,连接![]() ,要证对任意的点
,要证对任意的点![]() 总有
总有![]() ,只要证出对于任意点M都有
,只要证出对于任意点M都有![]() 即可;由对称和旋转的性质易得
即可;由对称和旋转的性质易得![]() ,根据三角形全等的判定定理得,只需
,根据三角形全等的判定定理得,只需![]() 即可,再根据线段的中点定义可得
即可,再根据线段的中点定义可得![]() ,由此即可得出
,由此即可得出![]() 的值.
的值.
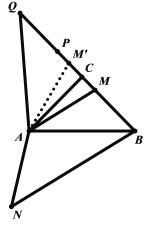
(1)由旋转的性质可得![]() ,再连接BN即可得,如下图所示:
,再连接BN即可得,如下图所示:
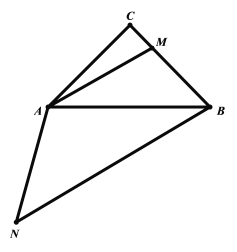
(2)等腰![]() 中,
中,![]()
![]()
又![]()
![]() ;
;
(3)![]() 时,对任意的点
时,对任意的点![]() 总有
总有![]() ,证明如下:
,证明如下:
如图,作点![]() 关于
关于![]() 的对称点
的对称点![]() ,连接
,连接![]()
设![]() (x的值随动点M的变动而变化),则
(x的值随动点M的变动而变化),则![]()
![]()
![]()
![]() ,即
,即![]()
![]() 垂直平分
垂直平分![]()
![]()
![]()
![]() ,即
,即![]()
由(2)知,![]()
![]()
在![]() 和
和![]() 中,
中,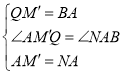
![]()
![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某校初三有2000名学生,为了解初三学生的体能,从人数相等的甲、乙两个班进行了抽样调查,过程如下,请补充完整.
收集数据:从甲、乙两个班各随机抽取20名学生.进行了体能测试,测试成绩(百分制)如下:
甲:78,86,74,81,75,76,87,70,75,90,75,79, 81,70, 74, 80 ,86, 69 ,83, 77.
乙:93,73,88,81,72,81,94,83,77,83,80,81,70,81,73,78,82,80,70,40.
整理、描述数据:按如下分数段整理、描述这两组样本数据:
成绩 |
|
|
|
|
|
|
甲班 | 0 | 0 | 1 | 11 | 7 | 1 |
乙班 | 1 | 0 | 0 | 7 | 10 | 2 |
(说明:成绩80分及以上为体能优秀,70~79分为体能良好,60~69分为体能合格,60分以下为体能不合格)
分析数据:两组样本数据的平均数、中位数、众数如下表所示:
班级 | 平均数 | 中位数 | 众数 | 优秀率 |
甲 | 78.3 | 77.5 | b | 40% |
乙 | 78 | a | 81 | c |
问题解决:
(1)表中a= ,b= ,c ;
(2)估计一下该校初三体能优秀的人数有多少人?
(3)通过以上数据的分析,你认为哪个班的学生的体能水平更高,并说明理由.
【题目】已知二次函数![]() .
.
(1)该二次函数的顶点坐标为__________;
(2)该函数的图象与![]() 轴的交点坐标为__________;
轴的交点坐标为__________;
(3)用五点法画函数图象
| … | … | |||||
| … | … |
(4)当![]() 时,则
时,则![]() 的取值范围是__________;
的取值范围是__________;
(5)将该抛物线绕顶点旋转180°,所得函数的解析式为__________;
(6)抛物线![]() 与
与![]() 轴有且仅有一个交点,则
轴有且仅有一个交点,则![]() __________.
__________.