题目内容
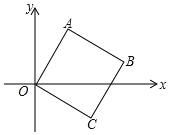
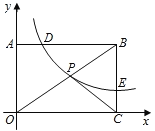
【题目】如图,已知矩形OABC中,OA=3,AB=4,双曲线y=![]() (k>0与矩形两边AB、BC分 别交于点D、E,且BD=2AD﹒
(k>0与矩形两边AB、BC分 别交于点D、E,且BD=2AD﹒
(1)求此双曲线的函数表达式及点E的坐标;
(2)若矩形OABC的对角线OB与双曲线相交于点P,连结PC,求△POC的面积﹒
【答案】(1)y=![]() , E(4,1); (2)S△OPC=2
, E(4,1); (2)S△OPC=2![]()
【解析】(1)由矩形OABC中,AB=4,BD=2AD,可得3AD=4,即可求得AD的长,然后求得点D的坐标,即可求得k的值,继而求得点E的坐标;
(2)先由点B的坐标得出OB的解析式,接着算出P的纵坐标,即可得出三角形OPC的面积.
(1)∵AB=4,BD=2AD,∴AB=AD+BD=AD+2AD=3AD=4,∴AD=![]() ,
,
又∵OA=3,所以D(![]() ,3),∵点D在双曲线y=
,3),∵点D在双曲线y=![]() 上,所以k=
上,所以k=![]() ×3=4.
×3=4.
∵四边形OABC为矩形,∴AB=OC=4,∴点E的横坐标为4.
把x=4代入y=![]() 中,得y=1,所以E(4,1).
中,得y=1,所以E(4,1).
(2)∵四边形OABC为矩形,OA=3,AB=4.
∴BC=OA=4,
∴B(4,3).
设直线OB的解析式为:y=![]() .
.
∵点P在双曲线y=![]() 和直线y=
和直线y=![]() 上.
上.
∴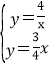 ,解得:
,解得: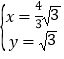 或
或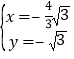 .
.
∵点P在第一象限,∴P的坐标为(![]() ).
).
∴S△POC=![]() =2
=2![]() .
.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目