Question

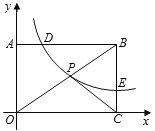
【题目】如图，在平面直角坐标系中，已知A(0，a)，B(b，0)，C(b，4)三点，其中a，b满足关系式a＝＋2.若在第二象限内有一点P(m，1)，使四边形ABOP的面积与三角形ABC的面积相等，则点P的坐标为(　　)

A. (－3，1) B. (－2，1) C. (－4，1) D. (－2.5，1)

Answer 1

【答案】A

【解析】

根据被开方数大于等于0，分母不等于0列式求出b，再求出a，从而得到A、B、C的坐标，再求出BC的长度，然后求出△ABC的面积，根据S四边形ABOP=S△AOP+S△AOB列式计算，然后列出方程求出m的值，从而得解．

由题意得，b2-9≥0且9-b2≥0，
解得，b2≥9且b2≤9，
所以，b2=9，
解得b=±3，
又∵b+3≠0，
解得b≠-3，
所以b=3，
a=2，
∴点A（0，2），B（3，0），C（3，4），
∴点B、C的横坐标都是3，
∴BC∥y轴，
∴BC=4-0=4，
△ABC的面积=×4×3=6，
∵OA=2，点P（m，）在第二象限，
∴S四边形ABOP=S△AOP+S△AOB，
=×2（-m）+×2×3，
=-m+3，
∵四边形ABOP的面积与△ABC的面积相等，
∴-m+3=6，
解得m=-3，
所以，点P（-3，）．
故选A．