Question

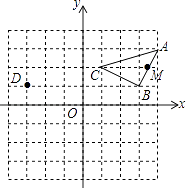
【题目】如图，在正方形ABCD中，AC为对角线，E为AB上一点，过点E作 EF∥AD，与AC、DC 分别交于点G，F，H为CG的中点，连结DE、 EH、DH、FH．下列结论：①EG=DF；②△EHF≌△DHC；③∠AEH+∠ADH=180°；④若，则．其中结论正确的有（ ）

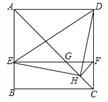
A. 1个 B. 2个 C. 3个 D. 4个

Answer 1

【答案】D

【解析】①根据题意可知∠ACD=45°，则GF=FC，则EG=EF-GF=CD-FC=DF；
②由SAS证明△EHF≌△DHC即可；
③根据△EHF≌△DHC，得到∠HEF=∠HDC，从而∠AEH+∠ADH=∠AEF+∠HEF+∠ADF-∠HDC=180°；
④若=，则AE=2BE，可以证明△EGH≌△DFH，则∠EHG=∠DHF且EH=DH，则∠DHE=90°，△EHD为等腰直角三角形，过H点作HM垂直于CD于M点，设HM=x，则DM=5x，DH=，CD=6x，则S△DHC=×HM×CD=3x2，S△EDH=×DH2=13x2．

①∵四边形ABCD为正方形,EF∥AD，

∴EF=AD=CD,∠ACD=45°,∠GFC=90°，

∴△CFG为等腰直角三角形，

∴GF=FC，

∵EG=EFGF，DF=CDFC，

∴EG=DF，故①正确；

②∵△CFG为等腰直角三角形，H为CG的中点，

∴FH=CH,∠GFH=∠GFC=45°=∠HCD，

在△EHF和△DHC中，

EF=CD；∠EFH=∠DCH；FH=CH，

∴△EHF≌△DHC(SAS)，故②正确；

③∵△EHF≌△DHC(已证)，

∴∠HEF=∠HDC，

∴∠AEH+∠ADH=∠AEF+∠HEF+∠ADF∠HDC=∠AEF+∠ADF=180°，故③正确；

④∵=，

∴AE=2BE，

∵△CFG为等腰直角三角形，H为CG的中点，

∴FH=GH,∠FHG=90°，

∵∠EGH=∠FHG+∠HFG=90°+∠HFG=∠HFD，

在△EGH和△DFH中，

EG=DF；∠EGH=∠HFD；GH=FH，

∴△EGH≌△DFH(SAS)，

∴∠EHG=∠DHF,EH=DH,∠DHE=∠EHG+∠DHG=∠DHF+∠DHG=∠FHG=90°,

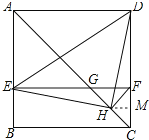
∴△EHD为等腰直角三角形，

如图，过H点作HM⊥CD于M，

设HM=x,则DM=5x,DH=，CD=6x，

则S△DHC=×HM×CD=3x2,S△EDH=×DH2=13x2，

∴3S△EDH=13S△DHC，故④正确；

故选：D.