题目内容
【题目】在平面直角坐标系中,对于任意一点P(x,y),我们做以下规定:d(P)=|x|+|y|,称d(P)为点P的坐标距离.
(1)已知:点P(3,﹣4),求点P的坐标距离d(P)的值.
(2)如图,四边形OABC为正方形,且点A、B在第一象限,点C在第四象限.
①求证:d(A)=d(C).
②若OC=2,且满足d(A)+d(C)=d(B)+2,求点B坐标.
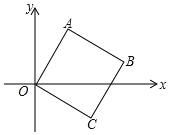
【答案】(1)7;(2)①见解析,②如图1所示,B(1+![]() ,
,![]() ﹣1).
﹣1).
【解析】
(1)根据d(P)=|x|+|y|,即可求得点P的坐标距离d(A);
(2)①证明:如图1,过点A作AE⊥y轴于E,作CF⊥y轴于F,则∠CFO=∠OEA=90°,设A(b,a),C(n,m),则|a|=OE,|b|=AE,|m|=OF,|n|=CF,根据相似三角形的性质得到![]() =1,求得
=1,求得![]() =1,于是得到
=1,于是得到![]() =1,即可得到结论;
=1,即可得到结论;
②如图1所示,过点B作BG⊥CF,交FC的延长线于G,交x轴于H,则GF=OH,GH=OF,∠G=∠AEO=90°,根据余角的性质得到∠BCG=∠COF,根据全等三角形的性质得到OE=BG,AE=CG,由图可得,d(A)=OE+AE,d(C)=OF+CF,d(B)=BH+OH=BH+GF,根据已知条件得到OE+AE+OF+CF=BH+GF+2,求得OF=1,解直角三角形得到CF=![]() ,由于
,由于![]() =1,求得BG=
=1,求得BG=![]() ,CG=1,于是得到结论.
,CG=1,于是得到结论.
(1)∵点P(3,﹣4),
∴点A的坐标距离d(P)=|3|+|﹣4|=3+4=7;
(2)①证明:如图1,过点A作AE⊥y轴于E,作CF⊥y轴于F,
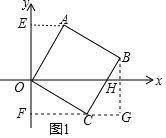
则∠CFO=∠OEA=90°,
设A(b,a),C(n,m),则|a|=OE,|b|=AE,|m|=OF,|n|=CF,
∵在正方形ABCO中,∠AOC=90°,
∴∠AOE+∠COF=90°,
又∵∠AOE+∠EAO=90°,
∴∠COF=∠OAE,
∴△CFO∽△OEA,
∴![]() =1,
=1,
∴![]() =1,即
=1,即![]() =1,
=1,
即|a|+|b|=|m|+|n|,
∴d(A)=d(C);
②如图1所示,过点B作BG⊥CF,交FC的延长线于G,交x轴于H,

则GF=OH,GH=OF,∠G=∠AEO=90°,
∵∠BCO=90°=∠CFO,
∴∠BCG+∠FCO=∠COF+∠FCO=90°,
∴∠BCG=∠COF,
∵∠COF=∠OAE,
∴∠BCG=∠OAE,
∵四边形ABCO是正方形,
∴CB=AO,
在△BCG和△OAE中,∠BCG=∠OAE;∠G=∠AEO;BC=AO,
∴△BCG≌△OAE(AAS),
∴OE=BG,AE=CG,
由图可得,d(A)=OE+AE,d(C)=OF+CF,d(B)=BH+OH=BH+GF,
∵d(A)+d(C)=d(B)+2,
∴OE+AE+OF+CF=BH+GF+2,
又∵BH=BGH=OEOF,GF=CG+CF=AE+CF,
∴OE+AE+OF+CF=(OEOF)+(AE+CF)+2,
∴即OF=2OF,
∴OF=1,
∵在Rt△COF中,CO=2,
∴CF=![]() ,
,
又∵![]() =1,
=1,
∴![]() ,即OE=
,即OE=![]() ,AE=1,
,AE=1,
∴BG=![]() ,CG=1,
,CG=1,
∴FG=CG+CF=1+![]() =OH,BH=BGOF=
=OH,BH=BGOF=![]() 1,
1,
∴B(1+![]() ,
,![]() 1).
1).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了15人某月的加工零件个数:
每人加工件数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数。
(2)若以本次统计所得的月加工零件数的平均数定为每位工人每月的生产定额,你认为这个定额是否合理,为什么?