题目内容
如图,在直角梯形ABCD中,∠A=90°,∠B=120°,AD= ,AB=6.在底边AB上有一动点E,满足∠DEQ=120°,EQ交射线DC于点F.
,AB=6.在底边AB上有一动点E,满足∠DEQ=120°,EQ交射线DC于点F.

(1)求下底DC的长度;
(2)当点E是AB的中点时,求线段DF的长度;
(3)请计算射线EF经过点C时,AE的长度.
 ,AB=6.在底边AB上有一动点E,满足∠DEQ=120°,EQ交射线DC于点F.
,AB=6.在底边AB上有一动点E,满足∠DEQ=120°,EQ交射线DC于点F.
(1)求下底DC的长度;
(2)当点E是AB的中点时,求线段DF的长度;
(3)请计算射线EF经过点C时,AE的长度.
(1)DC=7 (2)DF=6 (3) AE=2或5
试题分析:解:(1)作点B到DC的垂线,交DC于G
在梯形ABCD中,因为∠A=90°
所以DG=AB=6
因为∠B=120°,所以∠C=60°
又因为AD=BF=

所以CG=1
所以DC="DG+GC=6+1=7"
(2)解:如图1,过E点作EG⊥DF,
∵E是AB的中点,
∴DG=3,
∴EG=AD=
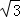 ,
,∴∠DEG=60°,
∵∠DEF=120°,
∴tan60°=
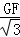 ,
, 解得GF=3,
∴DF=6;
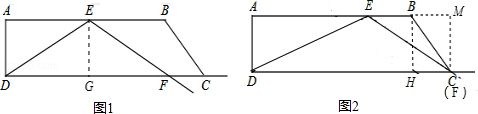
(3)如图2所示:
过点B作BH⊥DC,,过点C作CM⊥AB交AB延长线于点M,则BH=AD=
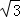 ,
,∵∠ABC=120°,AB∥CD,
∴∠BCH=60°,
∴CH=
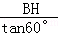 =
= =1,BC=
=1,BC=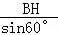 =
=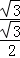 =2,
=2,设AE=x,则BE=6-x,
在R t △ADE中,DE=
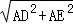 =
=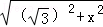 =
=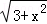 ,
,在R t △EFM中,EF=
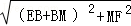 =
= =
=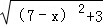 ,
,∵AB∥CD,
∴∠EFD=∠BEC,
∵∠DEF=∠B=120°,
∴△EDF∽△BCE,
∴
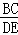 =
=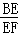 ,即
,即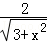 =
=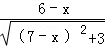 ,
,解得x=2或5.
∴AE=2或5.
点评:该题主要考查学生对勾股定理和直角梯形性质的理解和应用,以及对特殊角、特殊三角形性质的运用。

练习册系列答案
相关题目
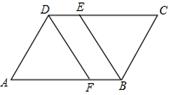



 的CD边上一点,连接BE,过点A作AF∥BE,交CD的延长线于点F,
的CD边上一点,连接BE,过点A作AF∥BE,交CD的延长线于点F,  的平分线分别交AF、AD于点G、H.
的平分线分别交AF、AD于点G、H.
 ,
, ,求
,求 的长度;
的长度; .
.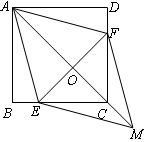

 中,D是AB中点,E是AC上的点,且
中,D是AB中点,E是AC上的点,且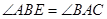 ,EF∥AB,DF∥BE,
,EF∥AB,DF∥BE,