题目内容
如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F.试判断AF与CE是否相等,并说明理由.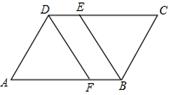

AF=CE
试题分析:根据平行四边形的性质可得AD=CB,∠A=∠C,∠ADC=∠ABC,再结合角平分线的性质可得∠ADF=∠CBE,即可根据“AAS”证得△ADF≌△CBE,问题得证.
AF=CE.理由如下:
∵四边形ABCD是平行四边形,
∴AD=CB,∠A=∠C,∠ADC=∠ABC
∵∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F
∴∠ADF=
 ∠ADC,∠CBE=
∠ADC,∠CBE= ∠ABC,
∠ABC,∴∠ADF=∠CBE,
∵在△ADF和△CBE中,
AD=CB,∠A=∠C,∠ADF=∠CBE
∴△ADF≌△CBE(AAS)
∴AF=CE.
点评:平行四边形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
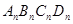 的面积为 .
的面积为 .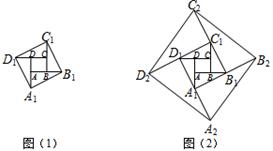
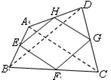




 CH.
CH.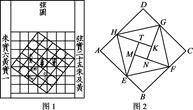

 ,AB=6.在底边AB上有一动点E,满足∠DEQ=120°,EQ交射线DC于点F.
,AB=6.在底边AB上有一动点E,满足∠DEQ=120°,EQ交射线DC于点F.