题目内容
已知:如图,在正方形ABCD中,点E、F分别在边BC和CD上,∠BAE=∠DAF.
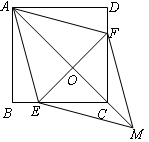
(1)求证:BE=DF;
(2)联结AC交EF于点O,延长OC至点M,使OM= OA,联结EM、FM.求证:四边形AEMF是菱形.

(1)求证:BE=DF;
(2)联结AC交EF于点O,延长OC至点M,使OM= OA,联结EM、FM.求证:四边形AEMF是菱形.
(1)先根据正方形的性质得到AB=AD,∠B=∠D=90°,再有∠BAE=∠DAF即可证得△ABE≌△ADF,从而得到结论;
(2)先根据正方形的性质得到∠BAC=∠DAC,再结合∠BAE=∠DAF可得∠EAO=∠FAO,由△ABE≌△ADF 可得AE=AF,根据等腰三角形三线合一的性质可得EO=FO,AO⊥EF,即可证得结论.
(2)先根据正方形的性质得到∠BAC=∠DAC,再结合∠BAE=∠DAF可得∠EAO=∠FAO,由△ABE≌△ADF 可得AE=AF,根据等腰三角形三线合一的性质可得EO=FO,AO⊥EF,即可证得结论.
试题分析:(1)∵正方形ABCD
∴AB=AD,∠B=∠D=90°
∵∠BAE=∠DAF
∴△ABE≌△ADF
∴BE=DF;
(2)∵正方形ABCD
∴∠BAC=∠DAC
∵∠BAE=∠DAF
∴∠EAO=∠FAO
∵△ABE≌△ADF
∴AE=AF
∴EO=FO,AO⊥EF
∵OM=OA
∴四边形AEMF是平行四边形
∵AO⊥EF
∴四边形AEMF是菱形.
点评:全等三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中极为重要的知识点,一般难度不大,需熟练掌握.

练习册系列答案
相关题目
 中,
中,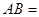 4,
4, 13,
13,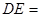 12,∠
12,∠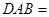
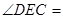 90°,∠
90°,∠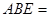 135°, 四边形
135°, 四边形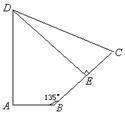

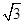 ,AB=6.在底边AB上有一动点E,满足∠DEQ=120°,EQ交射线DC于点F.
,AB=6.在底边AB上有一动点E,满足∠DEQ=120°,EQ交射线DC于点F.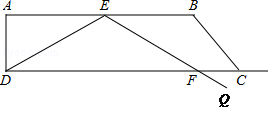
 ABCD的周长为16 cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
ABCD的周长为16 cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( ) 
 中,
中,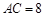 ,
, ,且
,且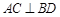 ,
,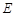 、
、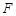 、
、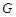 、
、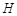 分别是
分别是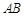 、
、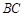 、
、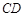 、
、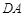 的中点,则
的中点,则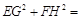 .
.