ЬтФПФкШн
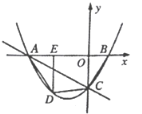
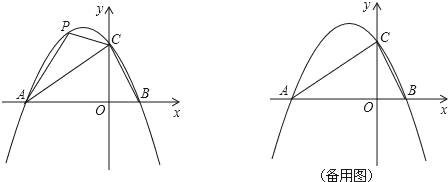
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЖўДЮКЏЪ§yЃНax2+bx+2ЕФЭМЯѓгыxжсНЛгкAЃЈЉ3ЃЌ0ЃЉЃЌBЃЈ1ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓетИіЖўДЮКЏЪ§ЕФЙиЯЕНтЮіЪНЃЛ
ЃЈ2ЃЉЕуPЪЧжБЯпACЩЯЗНЕФХзЮяЯпЩЯвЛЖЏЕуЃЌЪЧЗёДцдкЕуPЃЌЪЙЁїACPЕФУцЛ§зюДѓЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкЦНУцжБНЧзјБъЯЕжаЃЌЪЧЗёДцдкЕуQЃЌЪЙЁїBCQЪЧвдBCЮЊбќЕФЕШбќжБНЧШ§НЧаЮЃПШєДцдкЃЌжБНгаДГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉДцдкЃЌЕуP
ЃЛЃЈ2ЃЉДцдкЃЌЕуP![]() ЃЌЪЙЁїPACЕФУцЛ§зюДѓЃЛЃЈ3ЃЉДцдкЕуQЃЌЪЙЁїBCQЪЧвдBCЮЊбќЕФЕШбќжБНЧШ§НЧаЮЃЎQЕузјБъЮЊЃКQ1ЃЈ2ЃЌ3ЃЉЃЌQ2ЃЈ3ЃЌ1ЃЉЃЌQ3ЃЈЉ1ЃЌЉ1ЃЉЃЌQ4ЃЈЉ2ЃЌ1ЃЉЃЎ
ЃЌЪЙЁїPACЕФУцЛ§зюДѓЃЛЃЈ3ЃЉДцдкЕуQЃЌЪЙЁїBCQЪЧвдBCЮЊбќЕФЕШбќжБНЧШ§НЧаЮЃЎQЕузјБъЮЊЃКQ1ЃЈ2ЃЌ3ЃЉЃЌQ2ЃЈ3ЃЌ1ЃЉЃЌQ3ЃЈЉ1ЃЌЉ1ЃЉЃЌQ4ЃЈЉ2ЃЌ1ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉжБНгАбЕуAЃЈЉ3ЃЌ0ЃЉЃЌBЃЈ1ЃЌ0ЃЉДњШыЖўДЮКЏЪ§yЃНax2+bx+2ЧѓГіaЁЂbЕФжЕМДПЩЕУГіХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшЕуPзјБъЮЊЃЈmЃЌnЃЉЃЌдђnЃНЉ![]() m2Љ
m2Љ![]() m+2ЃЌСЌНгPOЃЌзїPMЁЭxжсгкMЃЌPNЁЭyжсгкNЃЎИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНЕУГіЁїPACЕФБэДяЪНЃЌдйИљОнЖўДЮКЏЪ§ЧѓзюДѓжЕЕФЗНЗЈЕУГіЦфЖЅЕузјБъМДПЩЃЛ
m+2ЃЌСЌНгPOЃЌзїPMЁЭxжсгкMЃЌPNЁЭyжсгкNЃЎИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНЕУГіЁїPACЕФБэДяЪНЃЌдйИљОнЖўДЮКЏЪ§ЧѓзюДѓжЕЕФЗНЗЈЕУГіЦфЖЅЕузјБъМДПЩЃЛ
ЃЈ3ЃЉвдBCЮЊБпЃЌдкЯпЖЮBCСНВрЗжБ№зїе§ЗНаЮЃЌе§ЗНаЮЕФЦфЫћЫФИіЖЅЕуОљПЩвдЪЙЕУЁАЁїBCQЪЧвдBCЮЊбќЕФЕШбќжБНЧШ§НЧаЮЁБЃЌвђДЫгаЫФИіЕуЗћКЯЬтвтвЊЧѓЃЌдйЙ§Q1ЕузїQ1DЁЭyжсгкЕуDЃЌЙ§ЕуQ2зїQ2EЁЭxжсгкЕуEЃЌИљОнШЋЕШШ§НЧаЮЕФХаЖЈЖЈРэЕУГіЁїQ1CDЁеЁїCBOЃЌЁїCBOЁеЁїBQ2EЃЌЙЪПЩЕУГіИїЕузјБъЃЎ
ЃЈ1ЃЉЁпХзЮяЯпyЃНax2+bx+2Й§ЕуAЃЈЉ3ЃЌ0ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЌ
Ёр![]()
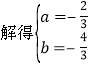
ЁрЖўДЮКЏЪ§ЕФЙиЯЕНтЮіЪНЮЊyЃНЉ![]() x2Љ
x2Љ![]() x+2ЃЛ
x+2ЃЛ
ЃЈ2ЃЉДцдкЃЎ
ЁпШчЭМ1ЫљЪОЃЌЩшЕуPзјБъЮЊЃЈmЃЌnЃЉЃЌдђnЃНЉ![]() m2Љ
m2Љ![]() m+2ЃЎ
m+2ЃЎ
СЌНгPOЃЌзїPMЁЭxжсгкMЃЌPNЁЭyжсгкNЃЎ
дђPMЃНЉ![]() m2Љ
m2Љ![]() m+2ЃЎЃЌPNЃНЉmЃЌAOЃН3ЃЎ
m+2ЃЎЃЌPNЃНЉmЃЌAOЃН3ЃЎ
ЁпЕБxЃН0ЪБЃЌyЃНЉ![]() ЁС0Љ
ЁС0Љ![]() ЁС0+2ЃН2ЃЌ
ЁС0+2ЃН2ЃЌ
ЁрOCЃН2ЃЌ
ЁрSЁїPACЃНSЁїPAO+SЁїPCOЉSЁїACO
ЃН![]() AOPM+
AOPM+![]() COPNЉ
COPNЉ![]() AOCO
AOCO
ЃН![]() ЁС3ЁСЃЈЉ
ЁС3ЁСЃЈЉ![]() m2Љ
m2Љ![]() m+2ЃЉ+
m+2ЃЉ+![]() ЁС2ЁСЃЈЉmЃЉЉ
ЁС2ЁСЃЈЉmЃЉЉ![]() ЁС3ЁС2
ЁС3ЁС2
ЃНЉm2Љ3m
ЁпaЃНЉ1ЃМ0
ЁрКЏЪ§SЁїPACЃНЉm2Љ3mгазюДѓжЕ
ЁрЕБmЃНЉ![]() ЃНЉ
ЃНЉ![]() ЪБЃЌSЁїPACгазюДѓжЕЃЎ
ЪБЃЌSЁїPACгазюДѓжЕЃЎ
ЁрnЃНЉ![]() m2Љ
m2Љ![]() m+2ЃНЉ
m+2ЃНЉ![]() ЁСЃЈЉ
ЁСЃЈЉ![]() ЃЉ2Љ
ЃЉ2Љ![]() ЁСЃЈЉ
ЁСЃЈЉ![]() ЃЉ+2ЃН
ЃЉ+2ЃН![]() ЃЌ
ЃЌ
ЁрДцдкЕуPЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЪЙЁїPACЕФУцЛ§зюДѓЃЎ
ЃЉЃЌЪЙЁїPACЕФУцЛ§зюДѓЃЎ
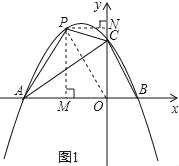
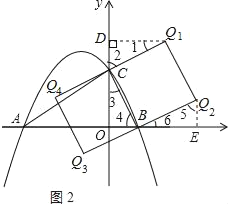
ЃЈ3ЃЉШчЭМ2ЫљЪОЃЌвдBCЮЊБпдкСНВрзїе§ЗНаЮBCQ1Q2ЁЂе§ЗНаЮBCQ4Q3ЃЌдђЕуQ1ЃЌQ2ЃЌQ3ЃЌQ4ЮЊЗћКЯЬтвтвЊЧѓЕФЕуЃЎЙ§Q1ЕузїQ1DЁЭyжсгкЕуDЃЌЙ§ЕуQ2зїQ2EЁЭxжсгкЕуEЃЌ
ЁпЁЯ1+ЁЯ2ЃН90ЁуЃЌЁЯ2+ЁЯ3ЃН90ЁуЃЌЁЯ3+ЁЯ4ЃН90ЁуЃЌ
ЁрЁЯ1ЃНЁЯ3ЃЌЁЯ2ЃНЁЯ4ЃЌ
дкЁїQ1CDгыЁїCBOжаЃЌ
Ёп ЃЌ
ЃЌ
ЁрЁїQ1CDЁеЁїCBOЃЌ
ЁрQ1DЃНOCЃН2ЃЌCDЃНOBЃН1ЃЌ
ЁрODЃНOC+CDЃН3ЃЌ
ЁрQ1ЃЈ2ЃЌ3ЃЉЃЛ
ЭЌРэПЩЕУQ4ЃЈЉ2ЃЌ1ЃЉЃЛ
ЭЌРэПЩжЄЁїCBOЁеЁїBQ2EЃЌ
ЁрBEЃНOCЃН2ЃЌQ2EЃНOBЃН1ЃЌ
ЁрOEЃНOB+BEЃН1+2ЃН3ЃЌ
ЁрQ2ЃЈ3ЃЌ1ЃЉЃЌ
ЭЌРэЃЌQ3ЃЈЉ1ЃЌЉ1ЃЉЃЌ
ЁрДцдкЕуQЃЌЪЙЁїBCQЪЧвдBCЮЊбќЕФЕШбќжБНЧШ§НЧаЮЃЎQЕузјБъЮЊЃКQ1ЃЈ2ЃЌ3ЃЉЃЌQ2ЃЈ3ЃЌ1ЃЉЃЌQ3ЃЈЉ1ЃЌЉ1ЃЉЃЌQ4ЃЈЉ2ЃЌ1ЃЉЃЎ

 ПЮЬУШЋНтзжДЪОфЖЮЦЊеТЯЕСаД№АИ
ПЮЬУШЋНтзжДЪОфЖЮЦЊеТЯЕСаД№АИ ВНВНИпПкЫуЬтПЈЯЕСаД№АИ
ВНВНИпПкЫуЬтПЈЯЕСаД№АИ ЕуОІаТНЬВФШЋФмНтЖСЯЕСаД№АИ
ЕуОІаТНЬВФШЋФмНтЖСЯЕСаД№АИ