题目内容
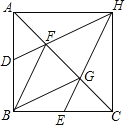
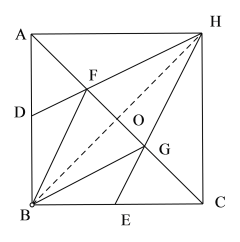
【题目】已知:如图,在△ABC中,AB=BC,∠ABC=90°,点D、E分别是边AB、BC的中点,点F、G是边AC的三等分点,DF、EG的延长线相交于点H,连接HA、HC.
(1)求证:四边形FBGH是菱形;
(2)求证:四边形ABCH是正方形.
【答案】(1)见解析 (2)见解析
【解析】
(1)由三角形中位线知识可得DF∥BG,GH∥BF,根据菱形的判定的判定可得四边形FBGH是菱形;
(2)连结BH,交AC于点O,利用平行四边形的对角线互相平分可得OB=OH,OF=OG,又AF=CG,所以OA=OC.再根据对角线互相垂直平分的平行四边形得证四边形ABCH是菱形,再根据一组邻边相等的菱形即可求解.
(1)∵点F、G是边AC的三等分点,
∴AF=FG=GC.
又∵点D是边AB的中点,
∴DH∥BG.
同理:EH∥BF.
∴四边形FBGH是平行四边形,
连结BH,交AC于点O,
∴OF=OG,
∴AO=CO,
∵AB=BC,
∴BH⊥FG,
∴四边形FBGH是菱形;
(2)∵四边形FBGH是平行四边形,
∴BO=HO,FO=GO.
又∵AF=FG=GC,
∴AF+FO=GC+GO,即:AO=CO.
∴四边形ABCH是平行四边形.
∵AC⊥BH,AB=BC,
∴四边形ABCH是正方形.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
【题目】某市水果批发部门欲将 A 市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为 200 元/ 时.其它主要参考数据如下:
运输工具 | 途中平均速度(千米/ 时) | 运费(元/ 千米) | 装卸费用(元) |
火车 | 100 | 15 | 2000 |
汽车 | 80 | 20 | 900 |
运输过程中,火车因多次临时停车,全程在路上耽误 2 小时 45 分钟,火车的总支出费用与汽车的总支出费用相同,请问某市与本地的路程是多少千米?