Question

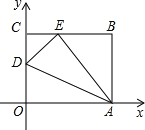
【题目】如图，四边形OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA＝10，OC＝8，在OC边上取一点D，将纸片沿AD翻折，点O落在BC边上的点E处．则直线DE的解析式为（　　）

A.y＝x+5B.y＝x+5C.y＝x+5D.y＝x+5

Answer 1

【答案】A

【解析】

首先在Rt△ABE中，求出EB，再在Rt△CDE中利用勾股定理即可求出D，E的坐标，从而求出直线解析式．

解：∵△ADE是由△ADO翻折，

∴DE＝DO，AO＝AE＝10，

∵四边形OABC是矩形，

∴OC＝AB＝8，AO＝BC＝10，∠B＝∠BCO＝∠BAO＝90°，

在Rt△ABE中，

∵AE＝10，AB＝8，

∴EB＝＝＝6，

∴EC＝4，

设DO＝DE＝x，

在Rt△DCE中，

∵CD2+CE2＝DE2，

∴（8﹣a）2+42＝a2，

∴a＝5，

∴点D（0，5），点E（4，8），

设直线DE为y＝kx+b，

∴,解得，

∴直线DE为：y＝+5,

故选：A．