题目内容
【题目】如图，已知，在锐角△ABC中，CE⊥AB于点E，点D在边AC上，联结BD交CE于点F，且EF·FC=FB·DF.
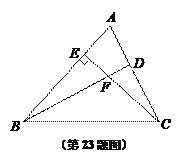
（1）求证：BD⊥AC；
（2）联结AF，求证：AF·BE=BC·EF.
【答案】（1）详见解析；（2）详见解析.
【解析】试题分析：（1）由两边成比例且夹角相等的两个三角形相似，可得△EFB∽△DFC，再由相似三角形对应角相等得∠FEB=∠FDC = 90°，即可得证；
（2）由△EFB∽△DFC得∠ABD =∠ACE，进而△AEC∽△FEB，由相似三角形对应边成比例得
，由此△AEF∽△CEB，可得
.
试题解析：（1）∵AF·BE=BC·EF ，
∴
，
∵ ∠EFB=∠DFC，
∴ △EFB∽△DFC.
∴ ∠FEB=∠FDC.
∵ CE⊥AB，
∴ ∠FEB= 90°.
∴ ∠FDC= 90°.
∴ BD⊥AC.
（2）∵ △EFB∽△DFC，
∴ ∠ABD =∠ACE.
∵ CE⊥AB，
∴ ∠FEB= ∠AEC= 90°.
∴ △AEC∽△FEB.
∴
,
∴
.
∵ ∠AEC=∠FEB= 90°，
∴ △AEF∽△CEB.
∴
，
∴
.
练习册系列答案
相关题目
