题目内容
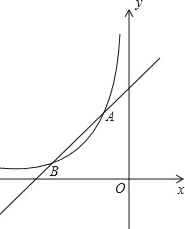
【题目】如图,函数![]() (x<0)与y=ax+b的图象交于点A(﹣1,n)和点B(﹣2,1).
(x<0)与y=ax+b的图象交于点A(﹣1,n)和点B(﹣2,1).
(1)求k,a,b的值;
(2)直线x=m与![]() (x<0)的图象交于点P,与y=﹣x+1的图象交于点Q,当∠PAQ>90°时,直接写出m的取值范围.
(x<0)的图象交于点P,与y=﹣x+1的图象交于点Q,当∠PAQ>90°时,直接写出m的取值范围.
【答案】(1)k=﹣2,a=1,b=3;(2)当m<﹣2或﹣1<m<0时,∠PAQ>90°.
【解析】试题分析:
(1)把点B的坐标代入![]() 即可求得k的值;再把点A的坐标代入所得反比例函数的解析式即可求得n的值;把A、B的坐标代入一次函数
即可求得k的值;再把点A的坐标代入所得反比例函数的解析式即可求得n的值;把A、B的坐标代入一次函数![]() 列出方程组,解方程组即可求得a、b的值;
列出方程组,解方程组即可求得a、b的值;
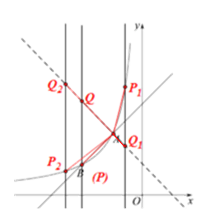
(2)如下图,由(1)可知一次函数![]() 的解析式为:
的解析式为: ![]() ,点A的坐标为(-1,2),由此可得:直线
,点A的坐标为(-1,2),由此可得:直线![]() 过点A,且直线
过点A,且直线![]() 垂直于直线
垂直于直线![]() ,垂足为点A,即∠QAB=90°,由下图可知,①当直线
,垂足为点A,即∠QAB=90°,由下图可知,①当直线![]() 在点B的左侧时,∠PAQ<90°;②当直线
在点B的左侧时,∠PAQ<90°;②当直线![]() 过点B时,∠PAQ=90°;③当直线
过点B时,∠PAQ=90°;③当直线![]() 在点B的右侧,点A左侧时,∠PAQ>90°;④当直线
在点B的右侧,点A左侧时,∠PAQ>90°;④当直线![]() 过点A时,P、A、Q三点重合;⑤当直线
过点A时,P、A、Q三点重合;⑤当直线![]() 在点A右侧,原点左侧时,∠P1AQ1>90°.综合可得当
在点A右侧,原点左侧时,∠P1AQ1>90°.综合可得当![]() ,且
,且![]() 时,∠PAQ>90°.
时,∠PAQ>90°.
试题解析:
(1)∵ 函数![]() (
(![]() )的图象经过点B(-2, 1),
)的图象经过点B(-2, 1),
∴![]() ,得
,得![]() .
.
∵ 函数![]() (
(![]() )的图象还经过点A(-1,n),
)的图象还经过点A(-1,n),
∴![]() ,点A的坐标为(-1,2).
,点A的坐标为(-1,2).
∵ 函数![]() 的图象经过点A和点B,
的图象经过点A和点B,
∴![]() 解得
解得![]()
(2)如下图,由(1)可知一次函数![]() 的解析式为:
的解析式为: ![]() ,点A的坐标为(-1,2),
,点A的坐标为(-1,2),
∴直线![]() 过点A,且直线
过点A,且直线![]() 垂直于直线
垂直于直线![]() ,垂足为点A,
,垂足为点A,
∴∠QAB=90°,
结合图形和已知条件分析可知,∠QAB的大小存在以下情形:①当直线![]() 在点B的左侧时,∠P2AQ2<90°;②当直线
在点B的左侧时,∠P2AQ2<90°;②当直线![]() 过点B时,∠PAQ=90°;③当直线
过点B时,∠PAQ=90°;③当直线![]() 在点B的右侧,点A左侧时,∠PAQ>90°;④当直线
在点B的右侧,点A左侧时,∠PAQ>90°;④当直线![]() 过点A时,P、A、Q三点重合;⑤当直线
过点A时,P、A、Q三点重合;⑤当直线![]() 在点A右侧,原点左侧时,∠P1AQ1>90°;
在点A右侧,原点左侧时,∠P1AQ1>90°;
综上所述,当![]() 且
且![]() 时,∠PAQ>90°.
时,∠PAQ>90°.

【题目】下表是某班体育考试跳绳项目模拟考试时10名同学的测试成绩(单位:个/分钟)
成绩(个/分钟) | 140 | 160 | 169 | 170 | 177 | 180 |
人数 | 1 | 1 | 1 | 2 | 3 | 2 |
则关于这10名同学每分钟跳绳的测试成绩,下列说法错误的是( )
A.方差是135B.平均数是170C.中位数是173.5D.众数是177