题目内容
【题目】如图,⊙O的直径AB=6cm,D为⊙O上一点,∠BAD=30°,过点D的切线交AB的延长线于点C.求∠ADC的度数及AC的长.
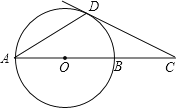
【答案】120°;9.
【解析】
试题分析:可通过构建直角三角形来求解.连接OD,那么OD⊥CD,这时∠ADC=∠ADO+90°,我们不难发现∠ADO=∠A=30°,因此∠DC=120°;根据三角形的内角和,那么∠C=30°,直角三角形ODC中,有OD的长,∠C=30°,可求出OC的值,也就求出了AC的长.
试题解析:(1)连接OD,
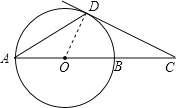
∵AO=OD,
∴∠ADO=∠DAO=30°,
∵CD是⊙O的切线,
∴∠CDO=90°,
∴∠ADC=∠ADO+∠CDO=30°+90°=120°;
(2)由(1)知∠COD=60°且OD=AO=![]() AB=3cm,
AB=3cm,
在Rt△COD中,∠C=30°,
∴OC=2OD=6cm,
∴AC=AO+OC=3+6=9cm.

练习册系列答案
相关题目