Question

【题目】在平面直角坐标系xOy中，直线y＝﹣x+m经过点A（2，0），交y轴于点B．点D为x轴上一点，且S△ADB＝1．

（1）求m的值；

（2）求线段OD的长；

（3）当点E在直线AB上（点E与点B不重合），且∠BDO＝∠EDA，求点E的坐标．

Answer 1

【答案】（1）2；（2）OD＝1或OD＝3；（3）点E的坐标为（，）或（，）

【解析】

（1）把点A的坐标代入直线解析式进行计算即可求出m的值；

（2）根据三角形的面积求出AD的长度，然后分点D在点A的左边与右边两种情况得到点D的坐标，再根据两点间的距离得到OD的长度；

（3）找出点B关于x轴的对称点B′，根据轴对称性作出∠BDO=∠EDA从而确定出点E的位置，再分点D的两种情况利用待定系数法求出直线B′D的解析式，然后联立直线AB的解析式，解方程组即可得到点E的坐标．

（1）∵直线y＝﹣x+m经过点A（2，0），

∴0＝﹣2+m，

∴m＝2；

（2）∵直线y＝﹣x+2交y轴于点B，

∴点B的坐标为（0，2），

∴OB＝2，

∵S△ADB＝ADOB＝1，

∴AD＝1，

∵点A的坐标为（2，0），

∴点D的坐标为（1，0）或（3，0），

∴OD＝1或OD＝3；

（3）①当点D的坐标为（1，0）时，如图所示，

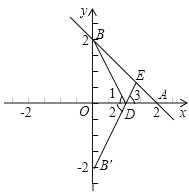
取点B′（0，﹣2），连接B′D并延长，交直线BA于点E．

∵OB＝OB′，AO⊥BB′于O，

∴OD为BB′的垂直平分线．

∴DB＝DB′，

∴∠1＝∠2．

又∵∠2＝∠3，

∴∠1＝∠3，

设直线B′D的解析式为y＝kx﹣2（k≠0），

∵直线B′D经过点D（1，0），

∴0＝k﹣2，

∴k＝2，

∴直线B′D的解析式为y＝2x﹣2，

联立得，

解得，

∴点E的坐标为（，）；

②当点D的坐标为（3，0）时，如图所示，

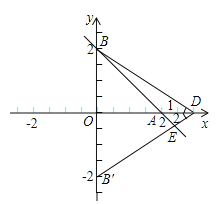
取点B′（0，﹣2），连接B′D，交直线BA于点E，

同①的方法，可得∠1＝∠2，直线B′D的解析式为y＝x﹣2，

联立得，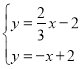

解得，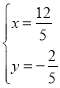

∴点E的坐标为（，），

综上所述，点E的坐标为（，）或（，）．