题目内容
【题目】如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,求壁虎捕捉蚊子的最短距离.(容器厚度忽略不计)

【答案】壁虎捕捉蚊子的最短距离为1.3m.
【解析】
将容器侧面展开,建立A关于EC的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.
解:如图:作A关于EC的对称点A′,连接A′B交EC于点F,则壁虎沿AF、FB捕捉蚊子距离最短.作A′D⊥BC交BC的延长线于D,则四边形A′DCE是矩形.
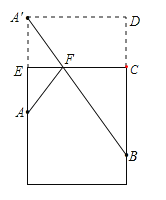
∵高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,壁虎离容器上沿0.3m处,
∴A′D=0.5m,A′E=AE=0.3m,BC=1.2-0.3=0.9m,
∴BD=BC+CD=0.9+0.3=1.2m,
∴A′B=![]() =
=![]() =1.3(m).
=1.3(m).
故壁虎捕捉蚊子的最短距离为1.3m.

练习册系列答案
相关题目