Question

【题目】在平面直角坐标系中，将某点（横坐标与纵坐标不相等）的横坐标与纵坐标互换后得到的点叫这个点的“互换点”，如（-3，5）与（5，-3）是一对“互换点”．

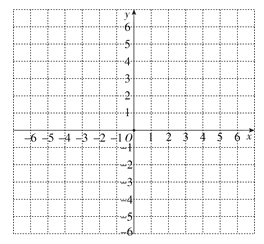
（1）以O为圆心，半径为5的圆上有无数对“互换点”，请写出一对符合条件的“互换点”；

（2）点M，N是一对“互换点”，点M的坐标为（m，n），且（m＞n），⊙P经过点M，N．

①点M的坐标为（4，0），求圆心P所在直线的表达式；

②⊙P的半径为5，求m－n的取值范围．

Answer 1

【答案】（1）答案不唯一，如：（4，3），（3，4）；（2）①y=x；②0＜m－n≤．

【解析】试题分析：根据“互换点”的定义，结合图形写出符合题意的点即可；（2）①因点M的坐标为（4，0），根据“互换点”的定义，点N的坐标为（0,4），由圆的对称性可知圆心P在直线OA上，从而可求圆心P所在直线的表达式；②由MN为⊙P直径时，求出m－n的最大值，由点M，N重合时，求出m－n的最小值.

解：（1）答案不唯一，如：（4，3），（3，4）；

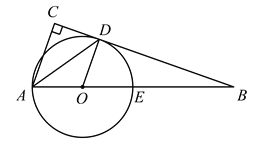
（2）①连结MN，∵OM=ON=4，∴Rt△OMN是等腰直角三角形．

过O作OA⊥MN于点A，∴点M，N关于直线OA对称．

由圆的对称性可知，圆心P在直线OA上，∴圆心P所在直线的表达式为y=x．

②当MN为⊙P直径时，由等腰直角三角形性质，可知m－n=；

当点M，N重合时，即点M，N横纵坐标相等，所以m－n=0；

∴m－n的取值范围是0＜m－n≤．