题目内容
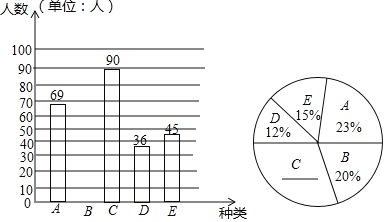
【题目】某中学为了了解在校学生对校本课程的喜爱情况,随机调查了九年级学生对A,B,C,D,E五类校本课程的喜爱情况,要求每位学生只能选择一类最喜欢的校本课程,根据调查结果绘制了如下的两个统计图.
请根据图中所提供的信息,完成下列问题:
(1)本次被调查的学生的人数为 ;
(2)补全条形统计图;
(3)扇形统计图中,C类所在扇形的圆心角的度数为 ;
(4)若该中学有4000名学生,请估计该校喜爱C,D两类校本课程的学生共有多少名.
【答案】(1)300;(2)见解析;(3)108°;(4)1680名.
【解析】
(1)根据A类的人数及其所占的百分比可得答案;
(2)用总人数乘以B类的人数所占的百分比可得出其人数,然后补全条形统计图;
(3)用360°乘以C类的人数所占的百分比可得答案;
(4)根据样本估计总体,利用总人数乘以C、D两类人数所占样本的比例可得答案.
解:(1)本次被调查的学生的人数为69÷23%=300(人),
故答案为:300;
(2)喜欢B类校本课程的人数为:300×20%=60(人),
补全条形图如下: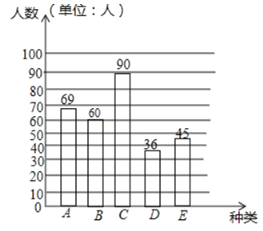
(3)扇形统计图中,C类所在扇形的圆心角的度数为360°×![]() =108°,
=108°,
故答案为:108°;
(4)∵4000×![]() =1680(名),
=1680(名),
答:估计该校喜爱C,D两类校本课程的学生共有1680名.

【题目】今年4月23日,是第16个世界读书日.某校为了解学生每周课余自主阅读的时间,在本校随机抽取若干名学生进行问卷调查,现将调查结果绘制成如图不完整的统计图表,请根据图表中的信息解答下列问题
组别 | 学习时间x(h) | 频数(人数) |
A | 0<x≤1 | 8 |
B | 1<x≤2 | 24 |
C | 2<x≤3 | 32 |
D | 3<x≤4 | n |
E | 4小时以上 | 4 |
(1)表中的n=_____,中位数落在_____组,扇形统计图中B组对应的圆心角为_____°;
(2)请补全频数分布直方图;
(3)该校准备召开利用课余时间进行自主阅读的交流会,计划在E组学生中随机选出两人进行经验介绍,已知E组的四名学生中,七、八年级各有1人,九年级有2人,请用画树状图法或列表法求抽取的两名学生都来自九年级的概率.