Question

【题目】 在△ABC中，AC=BC，∠ ACB=90°，AD平分∠BAC交BC边于点D，过B 作BH⊥AD，交AC的延长线于点E，H为垂足.

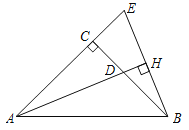
（1）求证： △ACD ≌ △BCE；

（2）找出BH和BC有怎样的数量关系（直接写出答案）

Answer 1

【答案】（1）证明见解析；（2）HB=BC．

【解析】

（1）先证明∠CAD=∠CBE，再根据“ASA”证明△ACD≌△BCE即可；

（2）根据“ASA”证明△AHE≌△AHB，得到EH=HB，AE=AB．设BH=x，BC=y，则BE=2x，AC=y，AE=AB=．在Rt△BCE中，根据勾股定理即可得到结论．

（1）∵∠ACB=90°，∴∠E+∠EBC=90°．

∵BH⊥AD，∴∠E+∠EAH=90°，∴∠EAH=∠EBC，∴∠CAD=∠CBE．

在△ACD和△BCE中，∵∠CAD=∠CBE，AC=BC，∠ACD=∠BCE=90°，∴△ACD≌△BCE（ASA）；

（2）∵AD平分∠BAC，∴∠EAH=∠BAH．

∵BH⊥AD，∴∠AHE=∠AHB．在△AHE和△AHB中，∵∠EAH=∠BAH，AH=AH，∠AHE=∠AHB，∴△AHE≌△AHB，∴EH=HB，AE=AB．

设BH=x，BC=y，则BE=2x，AC=y，AE=AB=．

在Rt△BCE中，∵BC2+CE2=BE2，∴，∴，∴，∴HB=BC．