题目内容
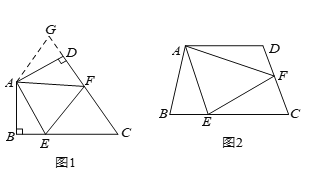
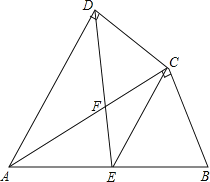
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求 ![]() 的值.
的值.
【答案】解:(1)证明:∵AC平分∠DAB,∴∠DAC=∠CAB。
∵∠ADC=∠ACB=90°,∴△ADC∽△ACB。
∴![]() ,即AC2=ABAD。
,即AC2=ABAD。
(2)证明:∵E为AB的中点,∴CE=![]() AB=AE。∴∠EAC=∠ECA。
AB=AE。∴∠EAC=∠ECA。
∵∠DAC=∠CAB,∴∠DAC=∠ECA。∴CE∥AD。
(3)∵CE∥AD,∴△AFD∽△CFE,∴![]() 。
。
∵CE=![]() AB,∴CE=
AB,∴CE=![]() ×6=3。
×6=3。
∵AD=4,∴![]() 。∴
。∴![]() 。
。
【解析】(1)由AC平分∠DAB,∠ADC=∠ACB=90°,可证得△ADC∽△ACB,然后由相似三角形的对应边成比例,证得AC2=ABAD。
(2)由E为AB的中点,根据在直角三角形中,斜边上的中线等于斜边的一半,即可证得CE=![]() AB=AE,从而可证得∠DAC=∠ECA,得到CE∥AD。
AB=AE,从而可证得∠DAC=∠ECA,得到CE∥AD。
(3)易证得△AFD∽△CFE,然后由相似三角形的对应边成比例,求得![]() 的值,从而得到
的值,从而得到![]() 的值。
的值。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】佳乐家超市元旦期间搞促销活动,活动方案如下表:
一次性购物 | 优惠方案 |
不超过200元 | 不给予优惠 |
超过200元,而不超过1000元 | 优惠10% |
超过1000元 | 其中1000元按8.5折优惠,超过部分按7折优惠 |
小颖在促销活动期间两次购物分别支付了134元和913元.
(1)小颖两次购买的物品如果不打折,应支付多少钱?
(2)在此活动中,他节省了多少钱?