题目内容
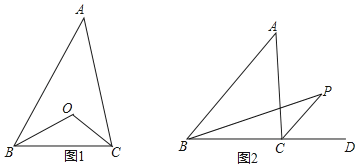
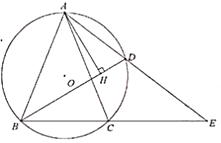
【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.

【答案】(1)证明见解析;(2)矩形ABCD的面积为![]() .
.
【解析】
(1)根据点F,H分别是BC,CE的中点,根据中位线的性质有FH∥BE,![]() .
.![]() .点G是BE的中点,
.点G是BE的中点,![]() .即可证明△BGF ≌ △FHC.
.即可证明△BGF ≌ △FHC.
(2)当四边形EGFH是正方形时,可知EF⊥GH且![]() 证明
证明![]() ,即可求出矩形的面积.
,即可求出矩形的面积.
【解答】(1)∵点F,H分别是BC,CE的中点,
∴FH∥BE,![]() .
.
∴![]() .
.
又∵点G是BE的中点,
∴![]() .
.
又∵![]() ,
,
∴△BGF ≌ △FHC.
(2)当四边形EGFH是正方形时,可知EF⊥GH且![]()
∵在△BEC中,点G,H分别是BE,EC的中点,
∴![]() 且GH∥BC,
且GH∥BC,
∴![]()
又∵AD∥BC, AB⊥BC,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目
【题目】佳乐家超市元旦期间搞促销活动,活动方案如下表:
一次性购物 | 优惠方案 |
不超过200元 | 不给予优惠 |
超过200元,而不超过1000元 | 优惠10% |
超过1000元 | 其中1000元按8.5折优惠,超过部分按7折优惠 |
小颖在促销活动期间两次购物分别支付了134元和913元.
(1)小颖两次购买的物品如果不打折,应支付多少钱?
(2)在此活动中,他节省了多少钱?