题目内容
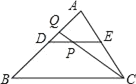
【题目】已知如图,DE是△ABC的中位线,点P是DE的中点,CP的延长线交AB于点Q,那么S△CPE:S△ABC=_____.
【答案】1:8.
【解析】
连结AP并延长交BC于点F,则S△CPE=S△AEP,可得S△CPE:S△ADE=1:2,由DE//BC可得△ADE∽△ABC,可得S△ADE:S△ABC=1:4,则S△CPE:S△ABC=1:8.
解:连结AP并延长交BC于点F,
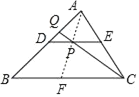
∵DE是△ABC的中位线,
∴E是AC的中点,
∴S△CPE=S△AEP,
∵点P是DE的中点,
∴S△AEP=S△ADP,
∴S△CPE:S△ADE=1:2,
∵DE是△ABC的中位线,
∴DE∥BC,DE:BC=1:2,
∴△ADE∽△ABC,
∴S△ADE:S△ABC=1:4,
∴S△CPE:S△ABC=1:8.
故答案为1:8.

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目