题目内容
【题目】如图,抛物线y=ax2+![]() x+c交x轴于A,B两点,交y轴于点C.直线y=﹣
x+c交x轴于A,B两点,交y轴于点C.直线y=﹣![]() +2经过点A,C.
+2经过点A,C.
(1)求抛物线的解析式;
(2)点P在抛物线在第一象限内的图象上,过点P作x轴的垂线,垂足为D,交直线AC于点E,连接PC,设点P的横坐标为m.
①当△PCE是等腰三角形时,求m的值;
②过点C作直线PD的垂线,垂足为F.点F关于直线PC的对称点为F′,当点F′落在坐标轴上时,请直接写出点P的坐标.
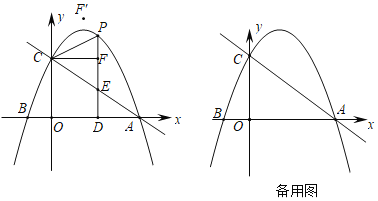
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)①当△PCE是等腰三角形时,m的值为m=4﹣
x+2;(2)①当△PCE是等腰三角形时,m的值为m=4﹣![]() ,2,
,2,![]() ;②点P的坐标为(1,3)或(
;②点P的坐标为(1,3)或(![]() ,
,![]() )
)
【解析】
(1)先由直线y=﹣![]() x+2求出A,C的坐标,再将其代入抛物线y=ax2+
x+2求出A,C的坐标,再将其代入抛物线y=ax2+![]() x+c中,即可求出抛物线解析式;
x+c中,即可求出抛物线解析式;
(2)①用含m的代数表示出P,E的坐标,再求出含m的代数式的PE的长度,将等腰三角形分三种情况进行讨论,即可分别求出m的值;
②当点F'落在坐标轴上时,存在两种情形,一种是点F'落在y轴上,一种是点F′落在x轴上,分情况即可求出点P的坐标.
解:(1)∵直线y=﹣![]() x+2经过A,C,
x+2经过A,C,
∴A(4,0),C(0,2),
∵抛物线y=ax2+![]() x+c交x轴于点B,交y轴于点C,
x+c交x轴于点B,交y轴于点C,
∴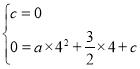 ,
,
∴a=﹣![]() ,c=2,
,c=2,
∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)∵点P在抛物线在第一象限内的图象上,点P的横坐标为m,
∴0<m<4,P(m,﹣![]() m2+
m2+![]() m+2),
m+2),
①∵PD⊥x轴,交直线y=﹣![]() x+2于点E,
x+2于点E,
∴E(m,﹣![]() m+2),
m+2),
∴PE=(﹣![]() m2+
m2+![]() m+2)﹣(﹣
m+2)﹣(﹣![]() m+2)=﹣
m+2)=﹣![]() m2+2m,
m2+2m,
∵PD∥CO,
∴![]() ,
,
∴CE=![]() =
=![]() m,
m,
当PE=CE时,﹣![]() m2+2m=
m2+2m=![]() m,
m,
解得,m1=4﹣![]() ,m2=0(舍去);
,m2=0(舍去);
当PC=CE时,PD+ED=2CO,
即(﹣![]() m2+
m2+![]() m+2)+(﹣
m+2)+(﹣![]() m+2)=2×2,
m+2)=2×2,
∴﹣![]() m2+m=0,
m2+m=0,
解得,m1=2,m2=0(舍去);
当PC=PE时,取CE中点G,则G(![]() m,﹣
m,﹣![]() m+2),PG⊥AC,
m+2),PG⊥AC,
∴∠GEP=∠OCA,
∴Rt△PGE∽Rt△AOC,
∴![]() =2,
=2,
∴(﹣![]() m2+
m2+![]() m+2)﹣(﹣
m+2)﹣(﹣![]() m+2)=2(m﹣
m+2)=2(m﹣![]() m),
m),
﹣![]() m2+
m2+![]() m=0,
m=0,
解得,m1=![]() ,m2=0(舍去),
,m2=0(舍去),
综上,当△PCE是等腰三角形时,m的值为m=4﹣![]() ,2,
,2,![]() ;
;
②P(1,3),P(![]() ,
,![]() ),理由如下,
),理由如下,
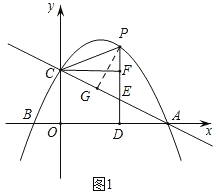
当点F'落在坐标轴上时,存在两种情形:
如图2﹣1,当点F'落在y轴上时,点P(m,﹣![]() m2+
m2+![]() m+2)在直线y=x
m+2)在直线y=x
+2上,
∴﹣![]() m2+
m2+![]() m+2=m+2,
m+2=m+2,
解得,m1=1,m2=0(舍去),
∴P(1,3);
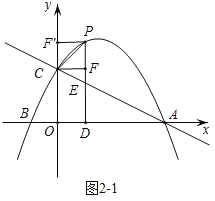
如图2﹣2,当点F'落在x轴上时,△COF'∽△F'DP,
∴![]() ,
,
∴![]() ,
,
∵PF=2﹣(﹣![]() m2+
m2+![]() m+2)=
m+2)=![]() m(m﹣3),
m(m﹣3),
∴F'D=![]() =m﹣3,
=m﹣3,
∴OF'=OD﹣FD=m﹣(m﹣3)=3,
在△CBF'中,CF'=![]() ,
,
∴m=![]() ,P(
,P(![]() ,
,![]() ),
),
综上所述,当点F′落在坐标轴上时,点P的坐标为(1,3)或(![]() ,
,![]() ).
).

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案【题目】在初中阶段的函数学习中,我们经历了“确定函数的解析式利用函数图象研究其性质﹣运用函数解决问题”的学习过程.在画函数图象时,我们可以通过描点或平移或翻折等方法画出函数图象、下面我们対函数y=|![]() ﹣1|展开探索,请补充以下探索过程:
﹣1|展开探索,请补充以下探索过程:
(1)列表
x | … | ﹣1 | ﹣ | ﹣ | ﹣ | 0 |
|
|
| … |
|
|
| 2 |
|
|
| 3 | … | |
y | … |
|
|
|
| 2 |
| 3 | a | … | 3 | 1 |
| 0 |
|
| b |
| … | |
直接写出函数自变量x的取值范围,及a= ,b= ;
(2)在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象,并写出这个函数的一条性质: .
(3)若方程|![]() ﹣1|=m有且只有一个解,直接写出m的值: .
﹣1|=m有且只有一个解,直接写出m的值: .