Question

【题目】抛物线y=x2+（2t﹣2）x+t2﹣2t﹣3与x轴交于A、B两点（A在B左侧），与y轴交于点C．

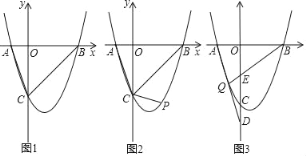
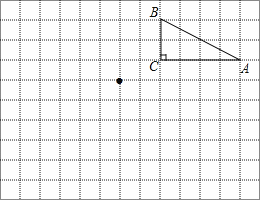
（1）如图1，当t=0时，连接AC、BC，求△ABC的面积；

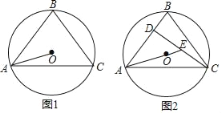
（2）如图2，在（1）的条件下，若点P为在第四象限的抛物线上的一点，且∠PCB+∠CAB=135°，求P点坐标；

（3）如图3，当﹣1＜t＜3时，若Q是抛物线上A、C之间的一点（不与A、C重合），直线QA、QB分别交y轴于D、E两点．在Q点运动过程中，是否存在固定的t值，使得CE=2CD．若存在，求出t值；若不存在，请说明理由．

Answer 1

【答案】（1）6．（2）（，﹣）．（3）t=．

【解析】

（1）代入t=0可得出抛物线的解析式，利用二次函数图象上点的坐标特征可求出点A，B，C的坐标，再利用三角形的面积公式即可求出△ABC的面积；
（2）由点B，C的坐标可得出∠ABC=45°，利用三角形内角和定理可得出∠ACB+∠CAB=135°，结合∠PCB+∠CAB=135°可得出∠ACB=∠PCB，过B作BM∥y轴，交CP延长线于M，由平行线的性质可得出∠ABC=∠MBC，结合BC=BC即可证出△ABC≌△MBC（ASA），利用全等三角形的性质可得出AB=MB=4，进而可得出点M的坐标，根据点C，M的坐标，利用待定系数法可求出直线CM的解析式，再联立直线CM及抛物线的解析式成方程组，通过解方程组可求出点P的坐标；
（3）利用二次函数图象上点的坐标特征及因式分解法解一元二次方程，可求出点A，B，C的坐标，设直线AQ的解析式为：y=k1x+b1，直线BQ的解析式为：y=k1x+b2，则CD=（t2-2t-3）-b1，CE=b2-（t2-2t-3），将直线解析式代入抛物线解析式中可得出关于x的一元二次方程，利用根与系数的关系可得出xAxQ=t2-2t-3-b1①，xBxQ=t2-2t-3-b2②，利用②÷①结合CE=2CD，即可得出关于t的方程，解之即可得出结论．

解：（1）将t=0代入抛物线解析式得：y=x2﹣2x﹣3．

当x=0时，y=x2﹣2x﹣3=﹣3，

∴点C的坐标为（0，﹣3）；

当y=0时，有x2﹣2x﹣3=0，

解得：x1=3，x2=﹣1，

∴点B的坐标为（3，0），点A的坐标为（﹣1，0）．

∴S△ABC= ABOC=×[3﹣（﹣1）]×3=6．

（2）由（1）知：B（3，0），C（0，﹣3），

∴OB=OC，

∴∠ABC=45°，

∴∠ACB+∠CAB=135°．

又∵∠PCB+∠CAB=135°，

∴∠ACB=∠PCB．

在图2中，过B作BM∥y轴，交CP延长线于M．

∴∠ABC=∠MBC．

在△ABC和△MBC中，，

∴△ABC≌△MBC（ASA），

∴AB=MB=4，

∴点M的坐标为（3，﹣4），

∴直线CM解析式为：y=﹣x﹣3（利用待定系数法可求出该解析式）．

联立直线CM及抛物线的解析式成方程组，得：，

解得：（舍去），，

∴点P的坐标为（，﹣）．

（3）当y=0时，有x2+（2t﹣2）x+t2﹣2t﹣3=0，即[x+（ t﹣3）][x+（ t+1）]=0，

解得：x1=﹣t+3，x2=﹣t﹣1，

∴点A的坐标为（﹣t﹣1，0），点B的坐标为（﹣t+3，0）．

当x=0时，y=x2+（2t﹣2）x+t2﹣2t﹣3=t2﹣2t﹣3，

∴点C的坐标为（0，t2﹣2t﹣3）．

设直线AQ的解析式为：y=k1x+b1，直线BQ的解析式为：y=k1x+b2．

∴点D的坐标为（0，b1），点E的坐标为（0，b2），

∴CD=（t2﹣2t﹣3）﹣b1，CE=b2﹣（t2﹣2t﹣3）．

∵y=k1x+b1，y=x2+（2t﹣2）x+t2﹣2t﹣3，

∴x2+（2t﹣2﹣k1）x+t2﹣2t﹣3﹣b1=0，

∴xAxQ=t2﹣2t﹣3﹣b1①．

同理：xBxQ=t2﹣2t﹣3﹣b2②．

由②÷①，得： ==﹣，

∴=﹣=2，

∴=﹣2，

∴t= ．