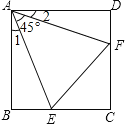
题目内容
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,以
上一动点,以![]() 为边向右侧作等边
为边向右侧作等边![]() ,点
,点![]() 的位置随点
的位置随点![]() 的位置变化而变化.
的位置变化而变化.
(1)如图1,当点![]() 在菱形
在菱形![]() 内部或边上时,连接
内部或边上时,连接![]() ,
,![]() 与
与![]() 的数量关系是 ,
的数量关系是 ,![]() 与
与![]() 的位置关系是 ;
的位置关系是 ;
(2)当点![]() 在菱形
在菱形![]() 外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
请说明理由(选择图2,图3中的一种情况予以证明或说理).
(3) 如图4,当点![]() 在线段
在线段![]() 的延长线上时,连接
的延长线上时,连接![]() ,若
,若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.

【答案】(1)BP=CE; CE⊥AD;(2)成立,理由见解析;(3)![]() .
.
【解析】(1)①连接AC,证明△ABP≌△ACE,根据全等三角形的对应边相等即可证得BP=CE;②根据菱形对角线平分对角可得![]() ,再根据△ABP≌△ACE,可得
,再根据△ABP≌△ACE,可得![]() ,继而可推导得出
,继而可推导得出![]() ,即可证得CE⊥AD;
,即可证得CE⊥AD;
(2)(1)中的结论:BP=CE,CE⊥AD 仍然成立,利用(1)的方法进行证明即可;
(3)连接AC交BD于点O,CE,作EH⊥AP于H,由已知先求得BD=6,再利用勾股定理求出CE的长,AP长,由△APE是等边三角形,求得![]() ,
, ![]() 的长,再根据
的长,再根据![]() ,进行计算即可得.
,进行计算即可得.
(1)①BP=CE,理由如下:
连接AC,
∵菱形ABCD,∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵△APE是等边三角形,
∴AP=AE ,∠PAE=60° ,
∴∠BAP=∠CAE,
∴△ABP≌△ACE,∴BP=CE;
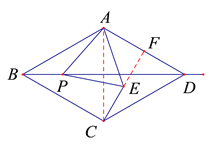
②CE⊥AD ,
∵菱形对角线平分对角,
∴![]() ,
,
∵△ABP≌△ACE,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴CF⊥AD ,即CE⊥AD;
(2)(1)中的结论:BP=CE,CE⊥AD 仍然成立,理由如下:
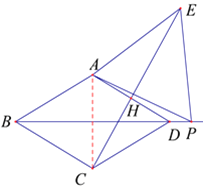
连接AC,
∵菱形ABCD,∠ABC=60°,
∴△ABC和△ACD都是等边三角形,
∴AB=AC,∠BAD=120° ,
∠BAP=120°+∠DAP,
∵△APE是等边三角形,
∴AP=AE , ∠PAE=60° ,
∴∠CAE=60°+60°+∠DAP=120°+∠DAP,
∴∠BAP=∠CAE,
∴△ABP≌△ACE,∴BP=CE,![]() ,
,
∴∠DCE=30° ,∵∠ADC=60°,
∴∠DCE+∠ADC=90° , ∴∠CHD=90° ,∴CE⊥AD,
∴(1)中的结论:BP=CE,CE⊥AD 仍然成立;
(3) 连接AC交BD于点O,CE,作EH⊥AP
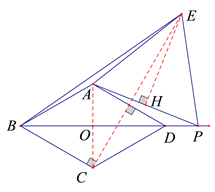
∵四边形ABCD是菱形,
∴AC⊥BD,BD平分∠ABC ,
∵∠ABC=60°,![]() ,
,
∴∠ABO=30° ,∴![]() , BO=DO=3,
, BO=DO=3,
∴BD=6,
由(2)知CE⊥AD,
∵AD∥BC,∴CE⊥BC,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
由(2)知BP=CE=8,∴DP=2,∴OP=5,
∴![]() ,
,
∵△APE是等边三角形,∴![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
=![]()
=![]()
=![]() ,
,
∴四边形ADPE的面积是![]() .
.