题目内容
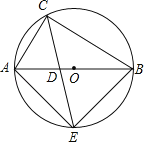
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,∠E=30°,AC=5.
(1)求CE的长;
(2)求S△ADC:S△ACE的比值.
【答案】(1)![]() ;(2)
;(2)![]() ﹣3.
﹣3.
【解析】
(1)先根据圆周角定理得出∠ACB=90°,由∠ABC=30°可得出AB的长,再由CE平分∠ACB得出∠BCE=∠BAE=45°,故可得出△ABE是等腰直角三角形,由勾股定理可得出AE的长;过点A作AF⊥CE于点F,△ACF为等腰直角三角形,由勾股定理得,AF和CF的长,再由勾股定理逆定理得EF的长,最后计算CE=CF+EF的长即可;(2)过点C作CM⊥AB于点M,连接OE,利用等底三角形的面积比等于高之比,得出![]() :
:![]() =
=![]() ,再通过比值计算即可得
,再通过比值计算即可得![]() :
:![]() 的比值.
的比值.
解:
(1)∵AB是⊙O的直径,
∴∠ACB=∠AEB=90°,
又∠E=30°,
∴∠ABC=30°,
∵AC=5,
∴AB=10,BC=![]() ,
,
∵CE平分∠ACB,
∴∠ACE=∠BCE=45°,AE=BE=![]() .
.
如图,过点A作AF⊥CE于点F,
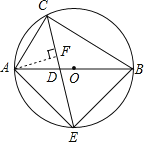
则△ACF为等腰直角三角形,
∴![]() ,
,
∴2CF2=25,
∴AF=CF=![]() ,
,
∴EF=![]()
![]() ,
,
∴CE=CF+EF=![]() ,
,
∴CE的长为![]() .
.
(2)过C作CM⊥AB于点M,连接OE,
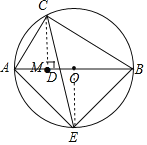
∵AE=BE,O为AB中点,
∴OE⊥AB,
∴S△ADC:S△ADE=CM:OE=CM:5,
∵ACBC=ABCM,
∴CM=![]() ,
,
∴S△ADC:S△ADE=![]() ,
,
∴S△ADC:S△ACE=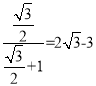 .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目