题目内容
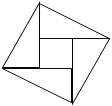
【题目】如图,下列四组条件中,能判定ABCD是正方形的有![]()
①AB=BC,∠BAD=90°; ![]() ;
;![]() ;
;![]() .
.

A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】分析:根据平行四边形的性质,矩形、菱形以及正方形的判定方法对各组条件进行判断即可得出答案.
详解:①AB=BC,![]()
根据有一个角是直角且有一组邻边相等的平行四边形是正方形,能判定ABCD是正方形,故此选项正确;
②AC⊥BD,AC=BD;
由对角线互相垂直的平行四边形是菱形,对角线相等的平行四边形是矩形,既是菱形又是矩形的四边形是正方形,能判定ABCD是正方形,故此选项正确;
③OA=OD,BC=CD;
由ABCD是平行四边形,可得AC与BD互相平分,而OA=OD,所以AC=BD,对角线相等的平行四边形是矩形,有一组邻边相等的平行四边形是菱形,既是矩形又是菱形的四边形是正方形,能判定ABCD是正方形,故此选项正确;
④![]()
由![]() ,根据对角线互相垂直的平行四边形是菱形,可得ABCD是菱形;由ABCD是平行四边形,可得AC与BD互相平分,AB∥CD,则∠ABD=∠CDB=∠DCA,所以OC=OD,又对角线相等的平行四边形是矩形,既是菱形又是矩形的四边形是正方形,能判定ABCD是正方形,故此选项正确。
,根据对角线互相垂直的平行四边形是菱形,可得ABCD是菱形;由ABCD是平行四边形,可得AC与BD互相平分,AB∥CD,则∠ABD=∠CDB=∠DCA,所以OC=OD,又对角线相等的平行四边形是矩形,既是菱形又是矩形的四边形是正方形,能判定ABCD是正方形,故此选项正确。
故选D.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目