题目内容
【题目】如图,在△ABC中,AB=AC,作AD⊥AB交BC的延长线于点D,作CE⊥AC,且使AE∥BD,连结DE.
(1)求证:AD=CE.
(2)若DE=3,CE=4,求tan∠DAE的值.

【答案】(1)证明见解析;
(2)tan∠DAE=![]() .
.
【解析】
试题分析:(1)利用已知条件证明△BAD≌△ACE,根据全等三角形的对应边相等即可解答;
(2)由△BAD≌△ACE,得到BD=AE,AD=CE,从而证明四边形ABDE为平行四边形,再证明∠EDA=∠BAD=90°,最后根据三角函数即可解答.
试题解析:(1)∵AB=AC,∴∠B=∠BCA,∵AE∥BD,∴∠CAE=∠BCA,∴∠B=∠CAE,又∵AD⊥AB,CE⊥AC,∴∠BAD=∠ACE=90°,
在△BAD和△ACE中,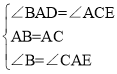 ,∴△BAD≌△ACE.∴AD=CE.
,∴△BAD≌△ACE.∴AD=CE.
(2)∵△BAD≌△ACE,∴BD=AE,AD=CE,∵AE∥BD,
∴四边形ABDE为平行四边形.∴DE∥AB,∴∠EDA=∠BAD=90°,
∴tan∠DAE=![]() .又∵AD=CE=4,DE=3,∴tan∠DAE=
.又∵AD=CE=4,DE=3,∴tan∠DAE=![]() =
=![]() .
.

练习册系列答案
相关题目