题目内容
已知二次函数的解析式为y=-x2+2x+1.
(1)写这个二次函数图象的对称轴和顶点坐标,并求图象与x轴的交点坐标;
(2)在给定的坐标系中画出这个二次函数大致图象,并求出抛物线与坐标轴的交点所组成的三角形的面积.

(1)写这个二次函数图象的对称轴和顶点坐标,并求图象与x轴的交点坐标;
(2)在给定的坐标系中画出这个二次函数大致图象,并求出抛物线与坐标轴的交点所组成的三角形的面积.

(1)∵y=-x2+2x+1=-(x-1)2+2,
∴对称轴为直线x=1,顶点坐标为(1,2),
令y=0,
则x1=1+
,x2=1-
,
∴抛物线与x轴的交点坐标为(1+
,0)、(1-
,0);
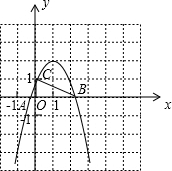
(2)二次函数的图象如图所示,
设抛物线与x轴的交点坐标为A和B,与y轴的交点为C,
∵A(1+
,0)、B(1-
,0);
∴AB=2
,OC=1,
∴S△ABC=
AB•OC
=
×2
×1
=
.
故答案为:(1+
,0)(1-
,0);
.
∴对称轴为直线x=1,顶点坐标为(1,2),
令y=0,
则x1=1+
| 2 |
| 2 |
∴抛物线与x轴的交点坐标为(1+
| 2 |
| 2 |

(2)二次函数的图象如图所示,
设抛物线与x轴的交点坐标为A和B,与y轴的交点为C,
∵A(1+
| 2 |
| 2 |
∴AB=2
| 2 |
∴S△ABC=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 2 |
=
| 2 |
故答案为:(1+
| 2 |
| 2 |
| 2 |

练习册系列答案
相关题目

 在x轴上,过A、B、C三点的抛物线表达式为
在x轴上,过A、B、C三点的抛物线表达式为


