题目内容
如图，抛物线y=x2-2x-3交x轴于A、B，交y轴于C，若在此抛物线上存在P，使△PAC的内心在x轴上，则点P的坐标为______．
y=0时，A（-1，0），B（3，0）
x=0时，C（0，-3）
∵三角形的内心在x轴上
∴∠PAB=∠BAC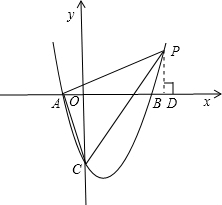
作PD⊥x轴于D，设P（x，y）
∴AD=x+1，PD=y
∵tan∠CAO=3
∴tan∠BAP=3
∴y=3（x+1）
∵y=x2-2x-3
解得：x=6或x=-1（不符合题意，应舍去）．
当x=6时，y=21，∴点P的坐标为（6，21）．
x=0时，C（0，-3）
∵三角形的内心在x轴上
∴∠PAB=∠BAC
作PD⊥x轴于D，设P（x，y）
∴AD=x+1，PD=y
∵tan∠CAO=3
∴tan∠BAP=3
∴y=3（x+1）
∵y=x2-2x-3
解得：x=6或x=-1（不符合题意，应舍去）．
当x=6时，y=21，∴点P的坐标为（6，21）．
练习册系列答案
相关题目
）两点，设OA•OB=3（O为坐标系原点）．
