题目内容
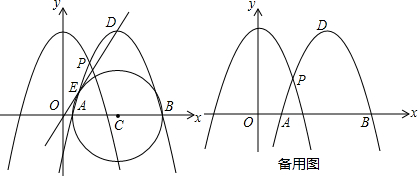
如图,在平面直角坐标系中有一直角梯形OABC,∠AOC=90°,AB∥OC,OC 在x轴上,过A、B、C三点的抛物线表达式为y=-
在x轴上,过A、B、C三点的抛物线表达式为y=-
x2+
x+10.
(1)求A、B、C三点的坐标;
(2)如果在梯形OABC内有一矩形MNPO,使M在y轴上,N在BC边上,P在OC边上,当MN为多少时,矩形MNPO的面积最大?最大面积是多少?
(3)若用一条直线将梯形OABC分为面积相等的两部分,试说明你的分法.
 在x轴上,过A、B、C三点的抛物线表达式为y=-
在x轴上,过A、B、C三点的抛物线表达式为y=-| 1 |
| 18 |
| 4 |
| 9 |
(1)求A、B、C三点的坐标;
(2)如果在梯形OABC内有一矩形MNPO,使M在y轴上,N在BC边上,P在OC边上,当MN为多少时,矩形MNPO的面积最大?最大面积是多少?
(3)若用一条直线将梯形OABC分为面积相等的两部分,试说明你的分法.
(1)由图形得,点A横坐标为0,将x=0代入y=-
x2+
x+10,
得y=10,
∴A(0,10)
∵AB∥OC,
∴B点纵坐标为10,将y=10代入抛物线表达式得,
10=-
x2+
x+10,
∴x1=0,x2=8.
∵B点在第一象限,
∴B点坐标为(8,10)
∵C点在x轴上,
∴C点纵坐标为0,将y=0代入抛物线表达式得,
-
x2+
x+10=0
解得x1=-10,x2=18.
∵C在原点的右侧,
∴C点坐标为(18,0). (4分)
(2)法一:过B作BQ⊥OC,交MN于H,交OC于Q,则Rt△BNH∽Rt△BCQ,
∴
=
. (5分)
设MN=x,NP=y,则有
=
.
∴y=18-x. (6分)
∴S矩形MNOP=xy=x(18-x)=-x2+18x=-(x-9)2+81.
∴当x=9时,有最大值81.
即MN=9时,矩形MNPO的面积最大,最大值为81. (8分)
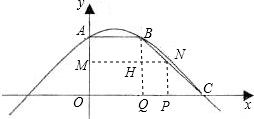
法二:过B作BQ⊥x轴于Q,则Rt△CPN∽Rt△CQB,
∴
=
.
设MN=x,NP=y,则有
=
.
∴y=18-x.
∴S矩形MNOP=xy=x(18-x)=-x2+18x=-(x-9)2+81.
∴当x=9时,有最大值81.
即MN=9时,矩形MNPO的面积最大,最大值为81.
法三:利用Rt△BHN∽Rt△NPC也能解答,解答过程与法二相同.
法四:过B点作BQ⊥x轴于Q,则Rt△BQC∽Rt△NPC,
QC=OC-OQ=18-8=10,又QB=OA=10,
∴△BQC为等腰直角三角形,
∴△NPC为等腰直角三角形.
设MN=x时矩形MNPO的面积最大.
∴PN=PC=OC-OP=18-x.
∴S矩形MNOP=MN•PN=x(18-x)=-x2+18x=-(x-9)2+81.
∴当x=9时,有最大值81.
即MN=9时,矩形MNPO的面积最大,最大值为81.
(3)①对于任意一条直线,将直线从直角梯形的一侧向另一侧平移的过程中,总有一个位置使得直线将该梯形面积分割
成相等的两部分.
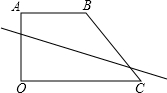
②过上、下底作一条直线交AB于E,交OC于F,且满足于梯形AEFO或梯形BEFC的上底与下底的和为13即可. (4分)
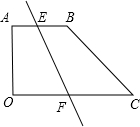
③构造一个三角形,使其面积等于整个梯形面积的一半,因此有:
△OCP1,P1(0,
);△OCP2,P2(
,
);△OAP3,P3(13,0);△CBP4,P4(5,0);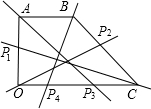
④平行于两底的直线,一定会有其中的一条将原梯形分成面积相等的两部分;
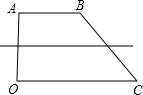
| 1 |
| 18 |
| 4 |
| 9 |
得y=10,
∴A(0,10)
∵AB∥OC,
∴B点纵坐标为10,将y=10代入抛物线表达式得,
10=-
| 1 |
| 18 |
| 4 |
| 9 |
∴x1=0,x2=8.
∵B点在第一象限,
∴B点坐标为(8,10)
∵C点在x轴上,
∴C点纵坐标为0,将y=0代入抛物线表达式得,
-
| 1 |
| 18 |
| 4 |
| 9 |
解得x1=-10,x2=18.
∵C在原点的右侧,
∴C点坐标为(18,0). (4分)
(2)法一:过B作BQ⊥OC,交MN于H,交OC于Q,则Rt△BNH∽Rt△BCQ,
∴
| BH |
| BQ |
| HN |
| QC |
设MN=x,NP=y,则有
| 10-y |
| 10 |
| x-8 |
| 18-8 |
∴y=18-x. (6分)
∴S矩形MNOP=xy=x(18-x)=-x2+18x=-(x-9)2+81.
∴当x=9时,有最大值81.
即MN=9时,矩形MNPO的面积最大,最大值为81. (8分)

法二:过B作BQ⊥x轴于Q,则Rt△CPN∽Rt△CQB,
∴
| CP |
| CQ |
| NP |
| BQ |
设MN=x,NP=y,则有
| 18-x |
| 18-8 |
| y |
| 10 |
∴y=18-x.
∴S矩形MNOP=xy=x(18-x)=-x2+18x=-(x-9)2+81.
∴当x=9时,有最大值81.
即MN=9时,矩形MNPO的面积最大,最大值为81.
法三:利用Rt△BHN∽Rt△NPC也能解答,解答过程与法二相同.
法四:过B点作BQ⊥x轴于Q,则Rt△BQC∽Rt△NPC,
QC=OC-OQ=18-8=10,又QB=OA=10,
∴△BQC为等腰直角三角形,
∴△NPC为等腰直角三角形.
设MN=x时矩形MNPO的面积最大.
∴PN=PC=OC-OP=18-x.
∴S矩形MNOP=MN•PN=x(18-x)=-x2+18x=-(x-9)2+81.
∴当x=9时,有最大值81.
即MN=9时,矩形MNPO的面积最大,最大值为81.
(3)①对于任意一条直线,将直线从直角梯形的一侧向另一侧平移的过程中,总有一个位置使得直线将该梯形面积分割
成相等的两部分.

②过上、下底作一条直线交AB于E,交OC于F,且满足于梯形AEFO或梯形BEFC的上底与下底的和为13即可. (4分)

③构造一个三角形,使其面积等于整个梯形面积的一半,因此有:
△OCP1,P1(0,
| 65 |
| 9 |
| 97 |
| 9 |
| 65 |
| 9 |

④平行于两底的直线,一定会有其中的一条将原梯形分成面积相等的两部分;


练习册系列答案
相关题目

 线y=-
线y=- 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. )两点,设OA•OB=3(O为坐标系原点).
)两点,设OA•OB=3(O为坐标系原点). 单位长度的速度从点A出发,沿A?B运动,连接PQ,CB,设点P的运动时间t秒.(0<t<2).
单位长度的速度从点A出发,沿A?B运动,连接PQ,CB,设点P的运动时间t秒.(0<t<2).