题目内容
【题目】如图，在平面直角坐标系中，四边形
是正方形，点
的坐标为
，弧
是以点
为圆心，
为半径的圆弧；弧
是以点
为圆心，
为半径的圆弧，弧
是以点
为圆心，
为半径的圆弧，弧
是以点为圆心，
为半径的圆弧.继续以点，，，为圆心按上述作法得到的曲线
…称为正方形的“渐开线”，则点
的坐标是__________．
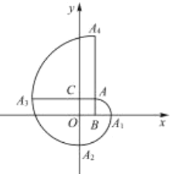
【答案】
【解析】
根据画弧的方法及其罗列的部分点的坐标发现：点Ax的坐标满足A4n=（1,4n+1）, A4n+1=（4n+2,0）A4n+2=（0,-（4n+2））A4n+3=（-（4n+3）,1），根据这一规律即可求出A2019的坐标.
观察规律：A(1,1),A1(2,0), A2(0,-2), A3(-3,1), A4(1,5)，A5(6,0)， A6(0，-6)
∴A4n=（1,4n+1）, A4n+1=（4n+2,0）A4n+2=（0,-（4n+2））A4n+3=（-（4n+3）,1），
∵2019÷4=504…3
∴A2019=（-（4n+3）,1）=
练习册系列答案
名师点拨卷系列答案
相关题目
