题目内容
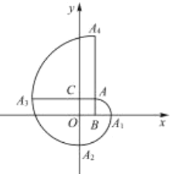
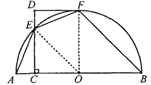
【题目】(本题10分)如图,AB是半圆O的直径,CD⊥AB于点C,交半圆于点E, DF切半圆于点F。已知∠AEF=135°。
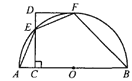
(1)求证:DF∥AB;
(2)若OC=CE,BF=![]() ,求DE的长。
,求DE的长。
【答案】见解析;2-![]()
【解析】
试题连结OF,根据切线得出DF⊥OF,根据内角四边形的性质以及∠AEF的度数得出∠B=45°,根据OB=OF得出∠FOA=90°,从而得出平行;连结OE,根据BF的长度和∠FOB=90°得出OB=OF=2,根据OC=CE,CE⊥AB,OE=OF=2得出CE的长度,根据DC∥OF,DF∥AB,∠COF=90°得出四边形COFD为矩形,从而得出DC=OF=2,然后根据DE=DC-CE求出答案.
试题解析:(1)连结OF ∵DF切半圆O于点F ∴DF⊥OF
∵∠AEF=135°,四边形ABFE为圆的内接四边形 ∴∠B=45° ∵OB=OF
∴∠FOA=90° ∴DF∥AB
(2)连结OE ∵BF=2![]() ∠FOB=90° ∴OB=OF=2
∠FOB=90° ∴OB=OF=2
∵OC=CE,CE⊥AB,OE=OF=2 ∴CE=![]() ∵DC∥OF,DF∥AB ∠COF=90°
∵DC∥OF,DF∥AB ∠COF=90°
∴四边形COFD为矩形 ∴DC=OF=2 ∴DE=DC-CE=2-![]()

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目